PQRS is a straight line. PQ = 2 cm and PS = 40 cm. If PR : RS = 7 : 3, then QR in cm is:
12
10
26
28
To solve the problem step by step, we will follow the information given in the question and the video transcript.
Step 1: Understand the given information
We have a straight line PQRS where:
- PQ = 2 cm
- PS = 40 cm
- The ratio PR : RS = 7 : 3
Step 2: Assign variables based on the ratio
Let:
- PR = 7x
- RS = 3x
Step 3: Write the equation for PS
Since PS is the total length from P to S, we can express it as:
PS=PR+RS
Substituting the values we assigned:
PS=7x+3x
PS=10x
Step 4: Set up the equation using the total length of PS
We know that PS = 40 cm, so we can set up the equation:
10x=40
Step 5: Solve for x
To find the value of x, we divide both sides of the equation by 10:
x=4010
x=4
Step 6: Calculate PR and RS
Now that we have the value of x, we can find PR and RS:
- PR = 7x = 7 * 4 = 28 cm
- RS = 3x = 3 * 4 = 12 cm
Step 7: Find QR
To find QR, we need to subtract PQ from PR:
QR=PR−PQ
Substituting the values:
QR=28−2
QR=26
Final Answer
The length of QR is 26 cm.
---
We have a straight line PQRS where:
- PQ = 2 cm
- PS = 40 cm
- The ratio PR : RS = 7 : 3
Let:
- PR = 7x
- RS = 3x
Since PS is the total length from P to S, we can express it as:
PS=PR+RS
Substituting the values we assigned:
PS=7x+3x
PS=10x
We know that PS = 40 cm, so we can set up the equation:
10x=40
To find the value of x, we divide both sides of the equation by 10:
x=4010
x=4
Now that we have the value of x, we can find PR and RS:
- PR = 7x = 7 * 4 = 28 cm
- RS = 3x = 3 * 4 = 12 cm
To find QR, we need to subtract PQ from PR:
QR=PR−PQ
Substituting the values:
QR=28−2
QR=26
The length of QR is 26 cm.
Topper's Solved these Questions
- RATIO AND PROPORTIONBOOK - BETOPPERSCHAPTER - RATIO AND PROPORTIONEXERCISE - IIT JEE WORKSHEET
1 Videos
- RATIO AND PROPORTIONBOOK - BETOPPERSCHAPTER - RATIO AND PROPORTIONEXERCISE - SUMMATIVE WORKSHEET
31 Videos
- NUMBER SYSTEM-IIBOOK - BETOPPERSCHAPTER - NUMBER SYSTEM-IIEXERCISE - IIT JEE WORKSHEET
51 Videos
Similar Questions
Knowledge Check
In a triangle PQR, PQ = 20 cm and PR = 6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of theseIn a triangle PQR, PQ=20 cm and PR =6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of the aboveΔPQR is right angled at point Q. If PQ=8cmand PR=(QR+2)cm. What is the value (in cm) of PR?
A17B15C19D18

The length of the straight line PQR is 22 cm. If PQ : QR m = 4: 7, find the length of PQ.
View SolutionIn the given figure, PQRS is a quadrilateral. If QR = 18 cm and PS = 9 cm, then what is the area (in cm2) of quadrilateral PQRS?
View SolutionΔPQR is right angled at point Q. If PQ=8cmand PR=(QR+2)cm. What is the value (in cm) of PR?
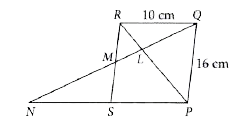
View SolutionIn the given figure , PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm . L is a point on PR such that RL:LP=2:3QL is produced to meet RS at M and PS produced at N . Find the length of PN and RM (in cm ) respectively .
View SolutionPQRS is an isosceles trapezium in which PS = 10 cm, PQ = SR = 13 cm and the distance between PS and QR is 12 cm. Find the area of the trapezium.
View Solution
