Prove that :
2C1+3C1+4C1=3C2+4C2.
The correct Answer is:9
To prove that (21)+(31)+(41)=(32)+(42), we will evaluate both sides of the equation.
Step 1: Evaluate the Left Hand Side (LHS)
The left-hand side is given by:
(21)+(31)+(41)
Using the property of combinations, we know that (n1)=n. Thus, we can calculate each term:
(21)=2,(31)=3,(41)=4
Now, substituting these values into the LHS:
LHS=2+3+4=9
Step 2: Evaluate the Right Hand Side (RHS)
The right-hand side is given by:
(32)+(42)
Again, using the formula for combinations, we can calculate each term:
(32)=3!2!(3−2)!=3!2!⋅1!=3×2×12×1×1=3
(42)=4!2!(4−2)!=4!2!⋅2!=4×3×2×1(2×1)(2×1)=124=6
Now, substituting these values into the RHS:
RHS=3+6=9
Step 3: Compare LHS and RHS
Now we compare both sides:
LHS=9andRHS=9
Since both sides are equal, we have:
(21)+(31)+(41)=(32)+(42)
Thus, we have proved the statement.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Frequently Asked Questions19videos
PERMUTATIONS AND COMBINATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Questions From NCERT Exemplar4videos
PERMUTATIONS AND COMBINATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - MOCK TESTEXERCISE - SECTION - D5videos
MOCK TEST
- BOOK - MODERN PUBLICATIONCHAPTER - PROBABILITYEXERCISE - CHAPTER TEST12videos
PROBABILITY
Similar Questions
Knowledge Check
- Question 1 - Select One
The sum of the series
3C0−4C1.12+5C2(12)2−6C3(12)3+... to ∞, isA16B8C1681Dnone of these
Prove that:
.2C2+3C2+4C2+…..+n+1C2=16n(n+1)(n+2)View SolutionProve that:
.2C2+3C2+4C2+…..+n+1C2=16n(n+1)(n+2)View SolutionIn C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
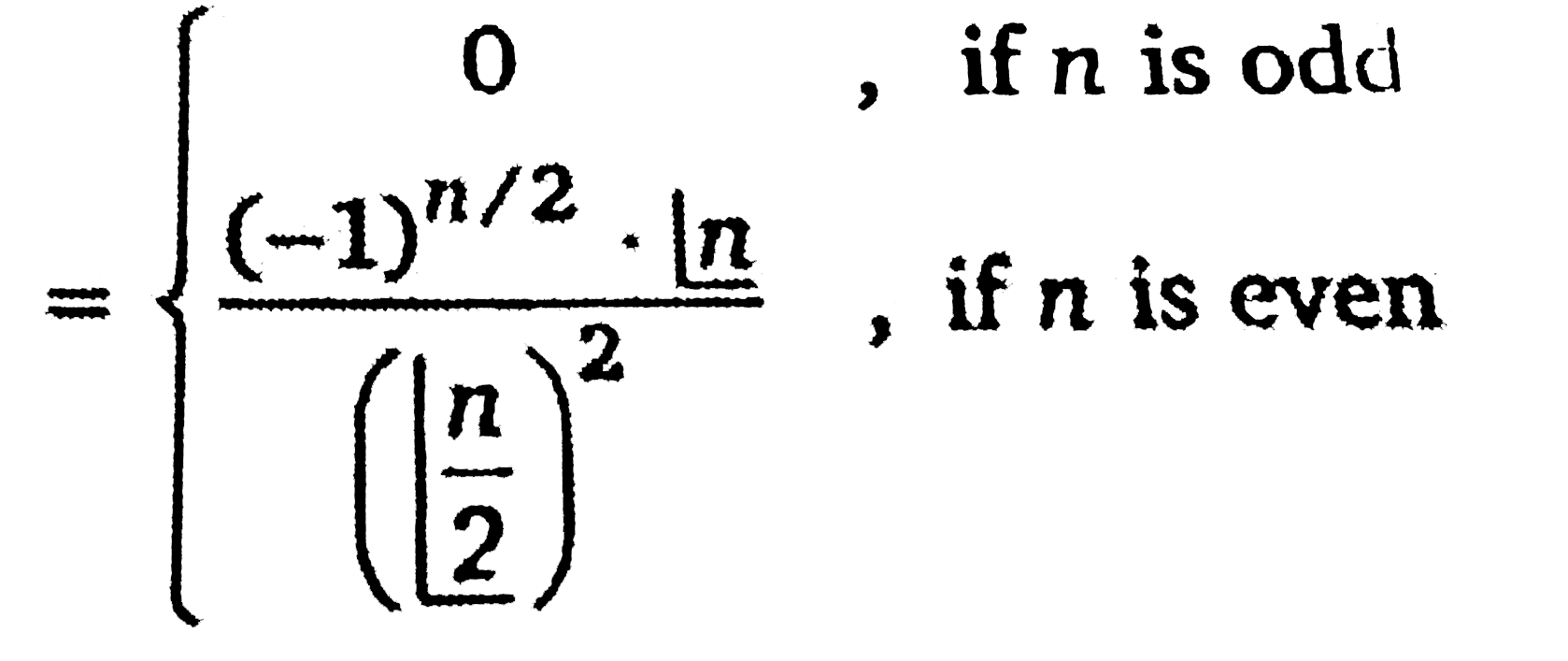
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
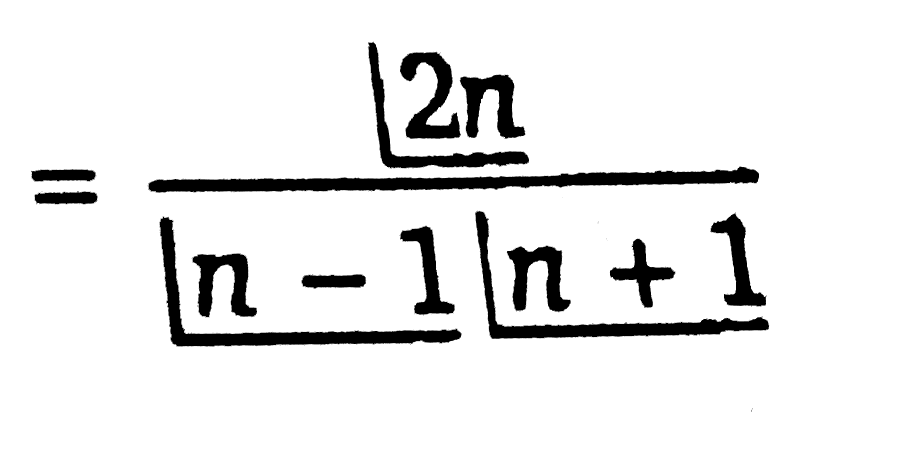 View Solution
View SolutionIf (1+x)n=C0+C1x+C2x2
+…+Cnxn, prove that +32⋅C3+…+n2⋅Cn
12⋅C1+22⋅C2=n(n+1)⋅2n−2 .View SolutionProve that
nC3+nC7+nC11+...=12{2n−1−2n/2sinnπ4}View SolutionIn C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
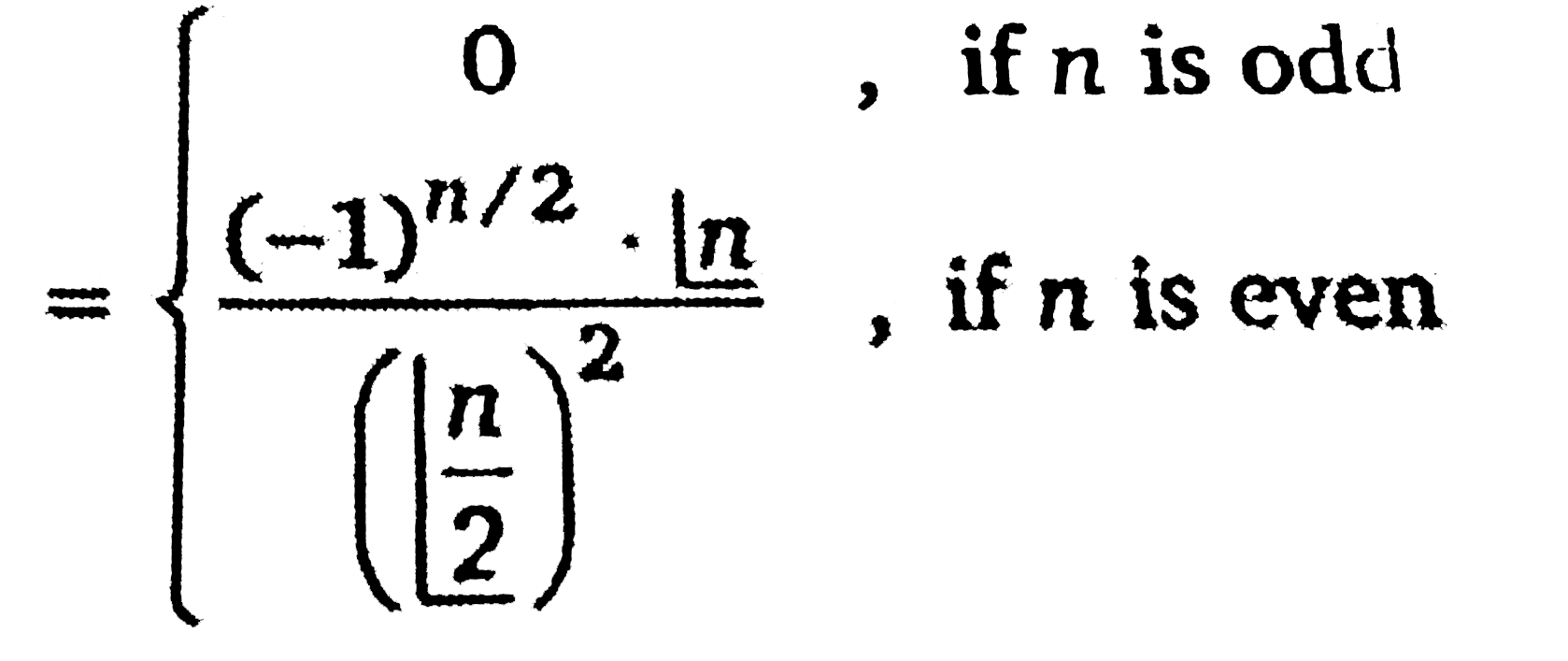
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
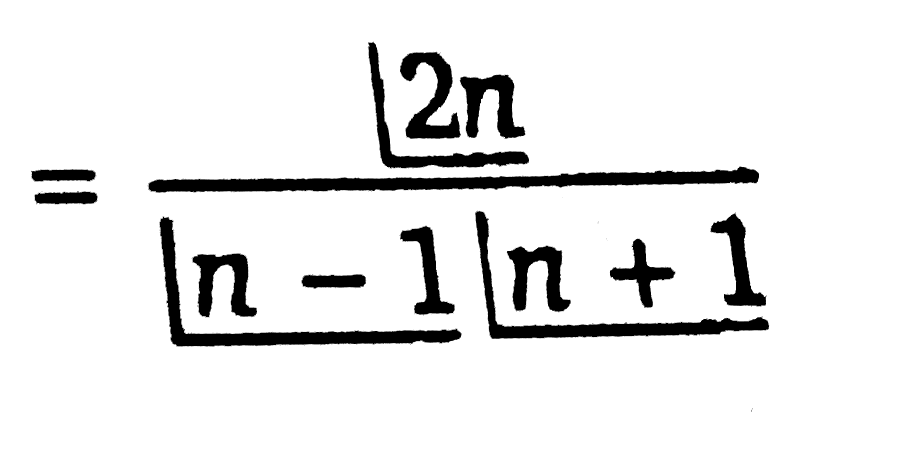 View Solution
View SolutionProve that C0−22C1+32C2−42C3++(−1)n(n+1)2×Cn=0whereCr=nCr .
View Solution

