Prove that a point can be found which is at the same distance from each of the four points : $(a m_{1}, \frac{a}{m_{1}}), (a m_{2}, \frac{a}{m_{2}}), (a m_{3}, \frac{a}{m_{3}}) and (\frac{a}{m_{1} m_{2} m_{3}}, a m_{1} m_{2} m_{3})$

Video Solution

Answer

Step by step video & image solution for Prove that a point can be found which is at the same distance from each of the four points :(a m_1, a/(m_1)), (a m_2, a/(m_2)),(a m_3, a/(m_3))"and"(a/(m_1m_2 m_3), a m_1m_2m_3) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Knowledge Check

If $m + 1 = \frac{5 (m - 1)}{3}$ , then $\frac{1}{m} =$
A $\frac{1}{4}$
B $\frac{3}{8}$
C $2$
D $\frac{8}{3}$

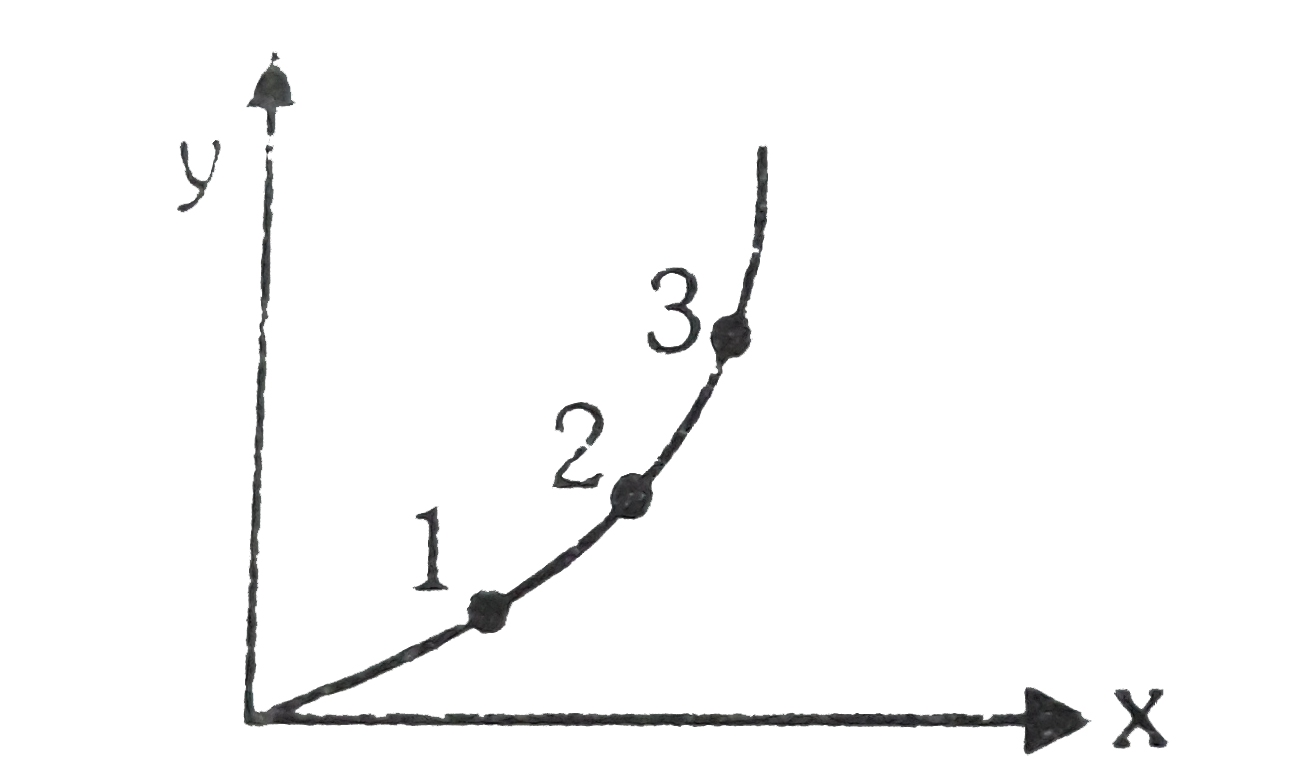
The slope of graph as shown in figure at points 1,2 and 3 is $m_{1}, m_{2}$ and $m_{3}$ respectively then

View Solution
Prove that the lengths of the perpendiculars from the points $(m^{2}, 2 m), (m m^{'}, m + m^{'}),$ and $(m^{' 2}, 2 m^{'})$ to the line $x + y + 1 = 0$ are in GP.
View Solution
If $\to a and \to b$ are two non-collinear vectors, show that points $l_{1} \to a + m_{1} \to b, l_{2} \to a + m_{2} \to b$ and $l_{3} \to a + m_{3} \to b$ are collinear if $∣ ∣ ∣ ∣ \begin{matrix} l_{1} & l_{2} & l_{3} m_{1} & m_{2} & m_{3} 1 & 1 & 1 \end{matrix} ∣ ∣ ∣ ∣ = 0 .$
View Solution
Prove that $(- a, - \frac{a}{2})$ is the orthocentre of the triangle formed by the lines $y = m_{i} x + \frac{a}{m_{i}}, I = 1, 2, 3, m_{1} m_{2} m_{3}$ being the roots of the equation $x^{3} - 3 x^{2} + 2 = 0$
View Solution
Prove that the lengths of the perpendiculars from the points $(m^{2}, 2 m), (m m^{'}, m + m^{'}),$ and $(m^{' 2}, 2 m^{'})$ to the line $x + y + 1 = 0$ are in GP.
View Solution
Show that the lines $y - m_{1} x - c_{1} = 0$ , $y - m_{2} x - c_{2} = 0$ and $y - m_{3} x - c_{3} = 0$ form an isosceles triangle with the first line as base if : $(1 + m_{1} m_{2}) (m_{1} - m_{3}) + (1 + m_{1} m_{3}) (m_{1} - m_{2}) = 0$
View Solution
Solve the linear equations. $m - \frac{m - 1}{2} = 1 - \frac{m - 2}{3}$
View Solution

Prove that a point can be found which is at the same distance from each of the four points : $(a m_{1}, \frac{a}{m_{1}}), (a m_{2}, \frac{a}{m_{2}}), (a m_{3}, \frac{a}{m_{3}}) and (\frac{a}{m_{1} m_{2} m_{3}}, a m_{1} m_{2} m_{3})$

Similar Questions

Knowledge Check

If $m + 1 = \frac{5 (m - 1)}{3}$ , then $\frac{1}{m} =$

Recommended Questions

Prove that a point can be found which is at the same distance from each of the four points :(am1,am1),(am2,am2),(am3,am3)and(am1m2m3,am1m2m3)

Similar Questions

Knowledge Check

If m+1=5(m−1)3, then 1m=

Recommended Questions

Prove that a point can be found which is at the same distance from each of the four points : $(a m_{1}, \frac{a}{m_{1}}), (a m_{2}, \frac{a}{m_{2}}), (a m_{3}, \frac{a}{m_{3}}) and (\frac{a}{m_{1} m_{2} m_{3}}, a m_{1} m_{2} m_{3})$

If $m + 1 = \frac{5 (m - 1)}{3}$ , then $\frac{1}{m} =$