Prove that a point can be found which is at the same distance from each of the four points :(am1,am1)⋅(am2,am2)⋅(am3,am3)and(am1m2m3,am1m2m3)
Step by step video & image solution for Prove that a point can be found which is at the same distance from each of the four points :(a m_1, a/(m_1))*(a m_2, a/(m_2))*(a m_3, a/(m_3))"and"(a/(m_1m_2 m_3), a m_1m_2m_3) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Area of triangle having angular points
A[am1m2,(m1+m2)],B[am2m3,a(m2+m3) and C[am3m1.a(m3+m1)] isA(m1−m2)(m2−m3)(m3−m1)Ba2(m1−m2)(m2−m3)(m3−m1)C12a2(m1−m2)(m2−m3)(m3−m1)Dnone of theseThe slope of graph as shown in figure at points 1, 2 and 3 is m1,m2andm3 respectively then
 Am1>m2>m3Bm1<m2<m3Cm1=m2=m3Dm1=m3>m2
Am1>m2>m3Bm1<m2<m3Cm1=m2=m3Dm1=m3>m2
238. EXAMPLE If the normals at three points P, Q and R in a s be the focus, meet point O and prove that SP. SQ. SR a SO As in the previous question we know that the normals a the points (ami, am 1), (am am2) and (am3, 2am3) meet in the point (h k), if m1 1m2 1m3 0 2a -h m2m3 m3m1 m1m2 (2)
View SolutionProve that the three lines from O with direction cosines l1,m1,n1:l2,m2,n2:l3,m3,n3 are coplanar, if l1(m2n3−n2m3)+m1(n2l3−l2n3)+n1(l2m3−l3m2)=0
View SolutionProve that the three lines from O with direction cosines l1,m1,n1:l2,m2,n2:l3,m3,n3 are coplanar, if l1(m2n3−n2m3)+m1(n2l3−l2n3)+n1(l2m3−l3m2)=0
View SolutionThe slope of graph as shown in figure at points 1,2 and 3 is m1,m2 and m3 respectively then
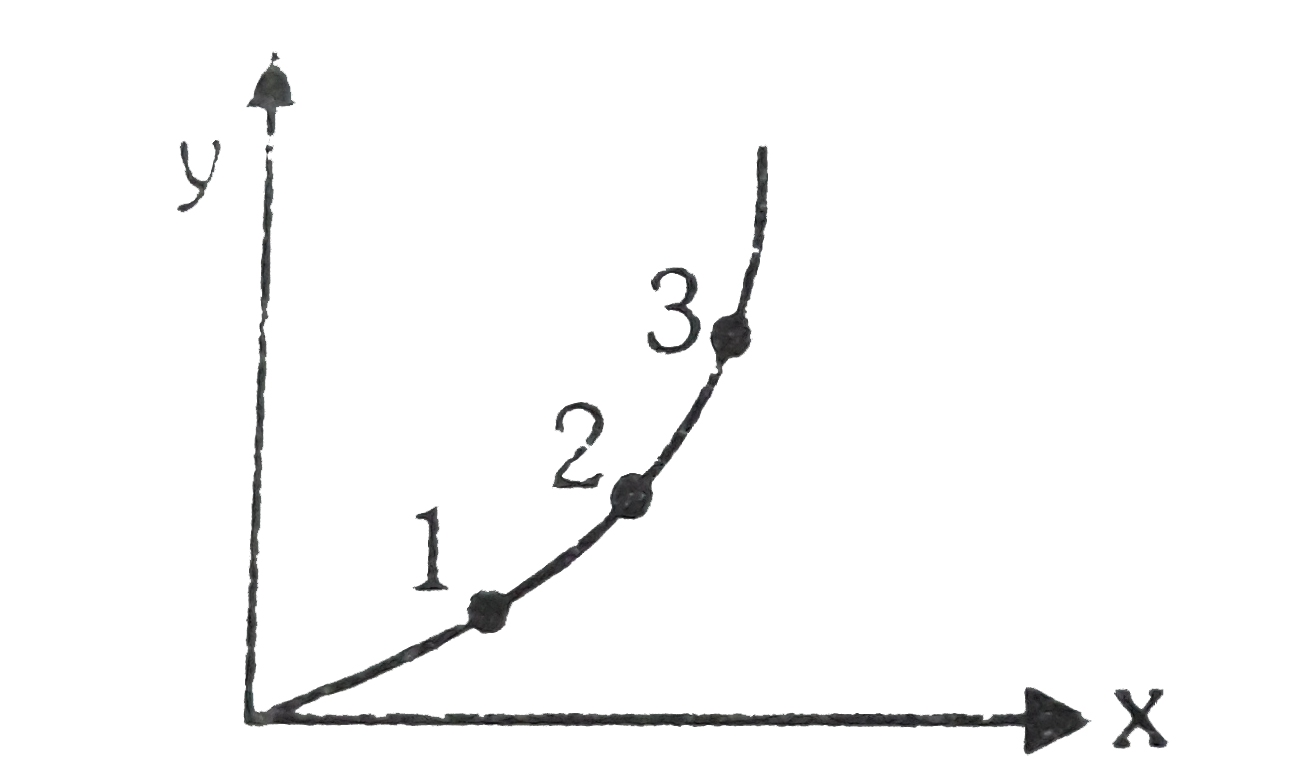
View SolutionThe slope of graph as shown in figure at points 1,2 and 3 is m1,m2 and m3 respectively then

View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View Solution
