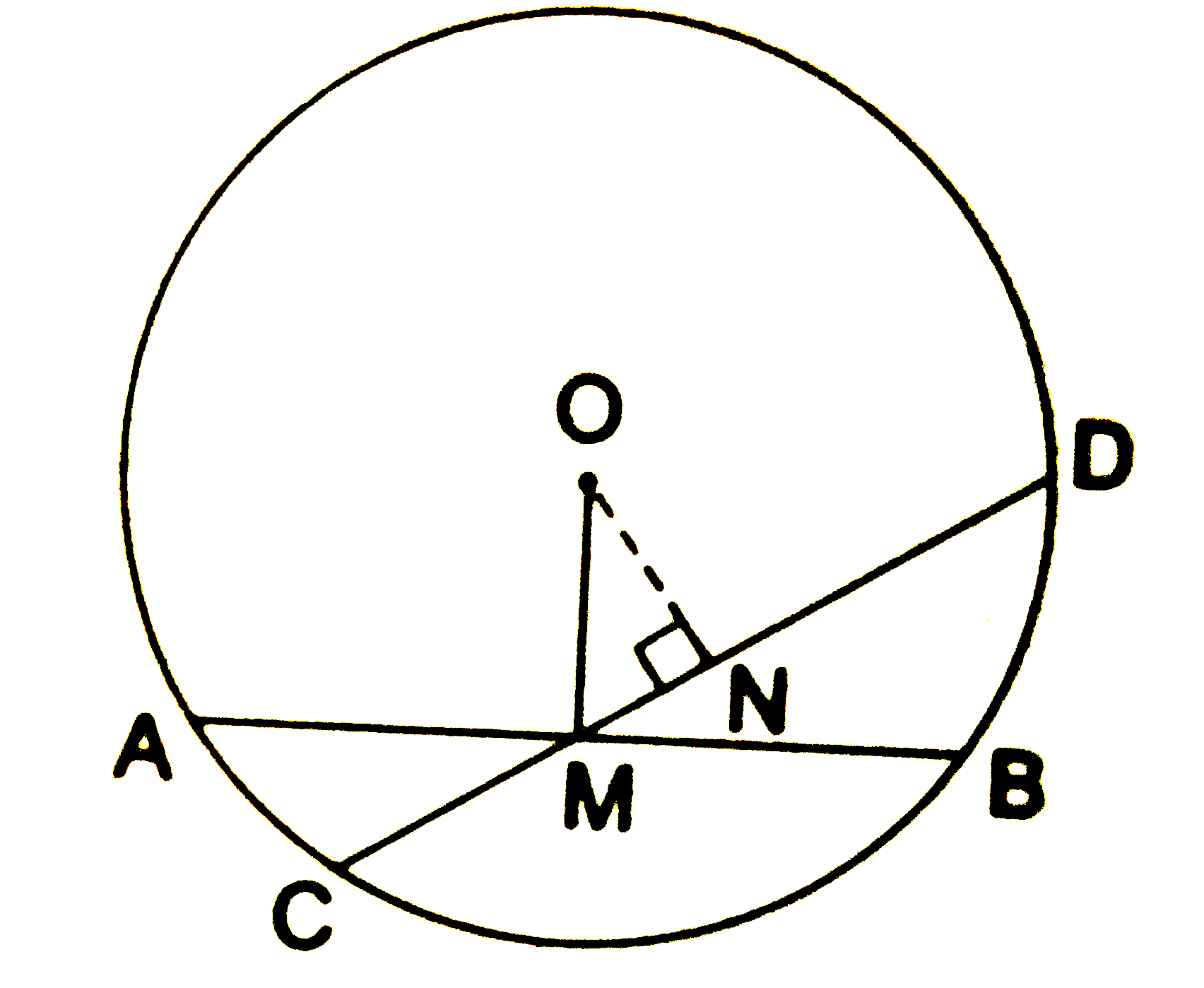
Prove that all the chords of a circle through a given point within it, the least is one which is bisected at that point.
Given A circle C(O,r) and a point M within it, AB is a chord with midpoint M and CD is another chrod through M.
To Prov AB<CD.
Construction Join OM and draw ON⊥CD.
Proof In the right ΔONM, OM is the hypotenus.
∴ON<OM
⇒ chord CD is nearer to O than chord AB.
We know that of any two chords of a circle, the one which is nearer to the centre is longer.
∴CD>AB
Hence, AB<CD
Thus, of all chords through M, the shortest is the one which is bisected at M.
Similar Questions
Knowledge Check
The equation of the chord of the circle x2+y2=81, which is bisected at the point (-2,3), is
A3x-y=13B3x-4y=13C3x-3y=13D2x-3y=-13
Prove that the locus of the point equidistant from two given points is the straight line which bisects the line segment joining the given points at right angles.
View SolutionIn two concentric circle, prove that a chord of larger circle which is tangent to smaller circle is bisected at the point of contact.
View SolutionProve that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
View SolutionShow that if two chords of a circle bisect one another they must be diameters.
View SolutionProve that the locus of the center of a circle, which intercepts a chord of given length 2a on the axis of x and passes through a given point on the axis of y distant b from the origin, is a parabola.
View SolutionProve that, through three given points which are not collinear, there is only one circle.
View SolutionProve that the equation of a line which passes through the given point (x1,y1)and is such that the given point bisects the part intercepted between the axis, is xx1+yy1=2
View Solution
