Prove that any four vertices of a regular pentagon are concyclic.
Given : A regular pentagon ABCDE.
To Prove : Every set of four vertices of ABCDE is a set of points lying on a circle.
Proof : First we show that the points A,B,C and E, lies on a circle.
Join AC and BE.
In ΔABC and ΔBAE, we have
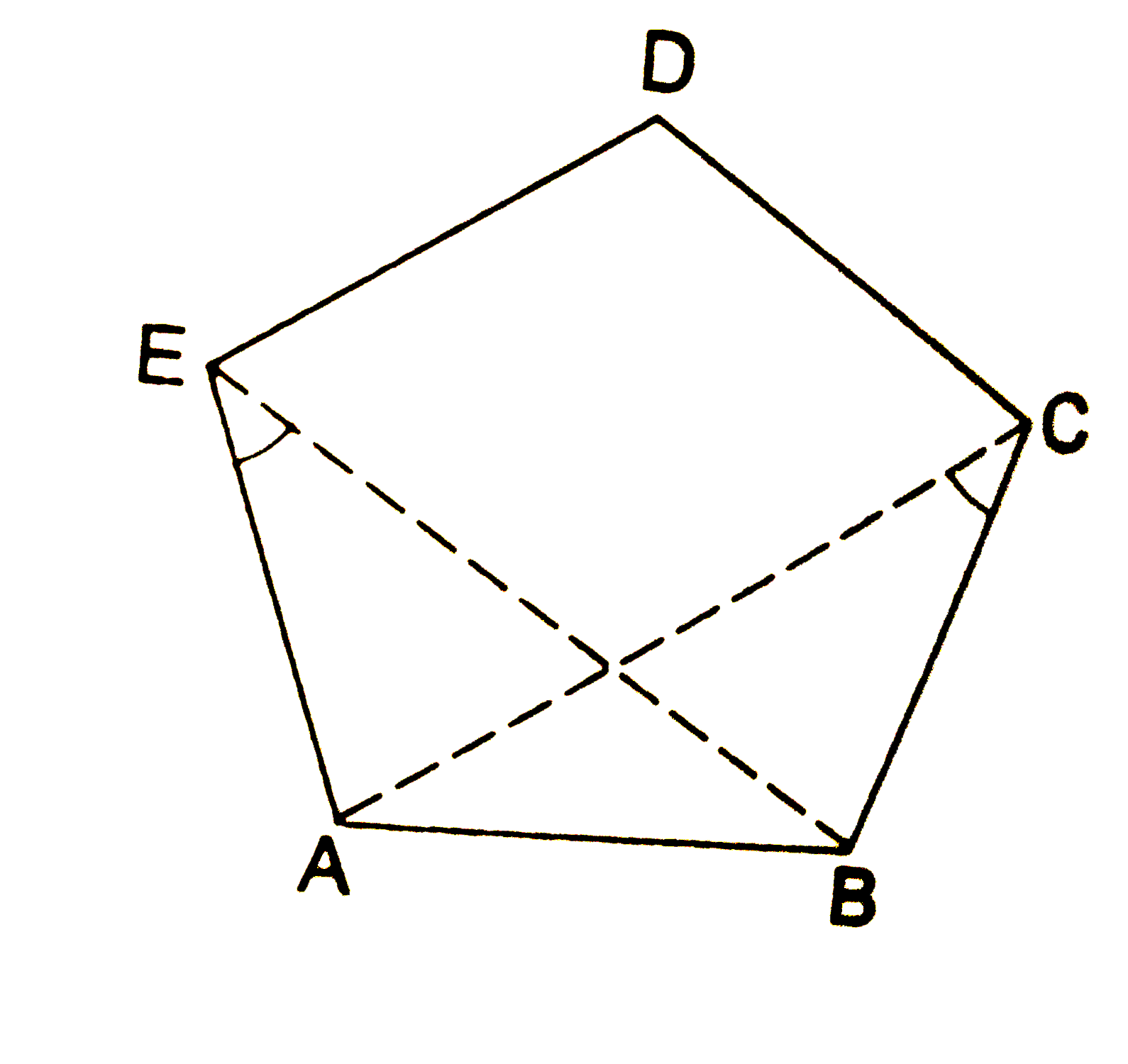
AB = BA [common ]
BC = AE [sides of a regular pentagon]
∠ABC=∠BAE [ each equal to 108∘]
∴ΔABC≅ΔBAE [ by SAS -congruence]
⇒∠BCA=∠AEB [ c.p.c.t.]
Thus, AB subtends equal angles at two points C and E on the same side of AB.
∴ the points A,B,C,E are concyclic. [ by Theorem 5 at Page 444].
Similary , every set of four vertices of pentagon ABCDE is a set of concyclic points.
Similar Questions
Knowledge Check
The least angle of rotation of a regular pentagon
A72∘B90∘C180∘D360∘Order of rotation of a regular pentagon is
A1B5C4D0Find each interior of a regular pentagon.
A108∘B105∘C103∘D101∘
Four particles each having a charge q are placed on the four vertices of a regular pentagon. The distance of each comer from !be centre is 'a'. Find the electric field at the centre of pentagon.
View SolutionFive point masses m each are kept at five vertices of a regular pentagon. Distance of centre of pentagon from any one of the verticle is 'a'. Find gravitational potential and filed strength at centre.
View SolutionProve that the interior angle of a regular pentagon is three times exterior anles of a regular decagon.
View SolutionFive identical charges, q1 each, are placed at the vertices of a regular pentagon having side length l1. The net electrostatic force on any of the charges due to other four is F1. Find the electrostatic force F2 on any one of the five identical charges, q2 each, placed at the vertices of a regular pentagon having side length l2.
View SolutionAssertion : Five charges +q each are placed at five vertices of a regular pentagon. A sixth xharge −Q is placed at the centre of pentagon. Then, net electrostatic force on −Q is zero.
Reason : Net electrostatic potential at the centre is zero.
View Solution
