Prove that Solution in Bengali
Consider p quantities each point equal to a and q quantities each equal to b. we know that
lt
Topper's Solved these Questions
- INEQUALITIES INVOLVING MEANS BOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Concept Application Eexercises 6.4
4 Videos
- INEQUALITIES INVOLVING MEANS BOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - EXERCISES (Single Correct answer type)
20 Videos
- INEQUALITIES INVOLVING MEANS BOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES INVOLVING MEANS EXERCISE - Concept Application Eexercises 6.2
6 Videos
- INEQUALITIES AND MODULUSBOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer
21 Videos
- INTEGRALSBOOK - CENGAGE PUBLICATIONCHAPTER - INTEGRALSEXERCISE - All Questions
762 Videos
Similar Questions
Prove that a4+b4+c4>abc(a+b+c),wherea,b,c>0.
View SolutionThe minimum value of x4+y4+z2xyz for positive real numbers x, y , z is
View SolutionProve that (n+12)n>n!
View SolutionIf f(x)=ax2+bx+c and f(−1)≥−4, f(1)≤0 and f(3)≥5, then the least value of a is
View SolutionIf ∫dxx2+ax+1=f(g(x))+c, then f(x) is inverse trigonometric function for |a|>2 f(x) is logarithmic function for |a|<2 g(x) is quadratic function for |a|>2 g(x) is rational function for |a|<2
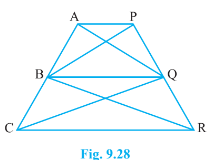
View SolutionIn Fig.9.28, AP || BQ || CR. Prove that ar (AQC) = ar (PBR).
View SolutionProve that apbq<(ap+bqp+q)p+q.
View SolutionIf P(A)=p and P(B)=q then
View SolutionIf p and q are primes such that p=q+2 prove that p^(p)+q^(q) is a multiple of p+q
View SolutionProve that q∧~p≡~(q→p)
View Solutionयदि किसी समांतर श्रेणी का p वां पद a और q वां पद b हो, तो सिद्ध करो कि p + q पदों का योगफल p+q2{a+b+a−bp−q} है।
View SolutionProve that q→p≡~p→~q
View SolutionProve that
Q→P≡P→−Q
View SolutionIf p<q, then p@q=p#q else p@q=q#p where a#b=ab. Then the value of (4@5)@(6@5) is :
View SolutionProve that apbq<(ap+bqp+q)p+q.
View SolutionIf a≠p,b≠q,c≠rand∣∣ ∣ ∣∣pbcaqcabr∣∣ ∣ ∣∣=0, then find the value of pp−a+qq−b+rr−c.
View Solution
