Prove that $a^{p} b^{q} < {(\frac{a p + b q}{p + q})}^{p + q} .$

Video Solution

|

Answer

Step by step video & image solution for Prove that a^p b^ q <((a p+b q)/(p+q))^(p+q)dot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 MATHS SEQUENCES AND SERIES

Similar Questions

Using truth table prove that $~ p \land q$
$\equiv (p \lor q) \land ~ p$
View Solution
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and Ris the mid-point of AP, show that (i) $a r (P R Q) = \frac{1}{2} a r (A R C)$ (ii) $a r (R Q C) = \frac{3}{8} a r (A B C)$ (iii) $a r (P B Q) = a r (A R C)$
View Solution
Prove that $q \land ~ p \equiv ~ (q \to p)$
View Solution
If the pth, qth and rth terms of a G.P. are a,b and c, respectively. Prove that
$a^{q - r} b^{r - p} c^{p - q} = 1$ .
View Solution
Without expanding, prove that $| a b c x y z p q r | = | x y z p q r a b c | = | y b q x a p z c r |$
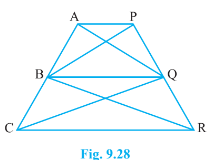
View Solution
In Fig.9.28, $A P | | B Q | | C R$ . Prove that $a r (A Q C) = a r (P B R) .$

View Solution
Using truth table prove that $p \lor (q \land r) \equiv (p \lor q) \land (p \lor r)$
View Solution
In A ABC , P and Q are respectively the mid-points of $A B$ and $B C$ and R is the mid-point of $A P .$ Prove that: $a r (P R Q) = \frac{1}{2} a r (A R C)$
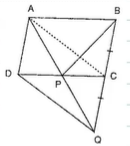
View Solution
In Figure, $A B C D$ is a parallelogram. Prove that: $a r (B C P) = a r (D P Q)$ CONSTRUCTION : Join $A C .$

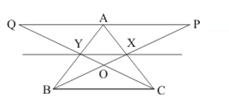
View Solution
In Figure, $X and Y$ are the mid-points of $A C and A B$ respectively, $Q P, B C and C Y Q and B X P$ are straight lines. Prove that $a r (A B P) = a r (A C Q)$
View Solution

Prove that apbq<(ap+bqp+q)p+q.

Similar Questions

Recommended Questions

Prove that $a^{p} b^{q} < {(\frac{a p + b q}{p + q})}^{p + q} .$