Prove that cos(tan−1(sin(cot−1x)))=√x2+1x2+2
Video Solution
Text Solution
E=cos(tan−1(sin(cot−1x)))
Let cot−1x=θ
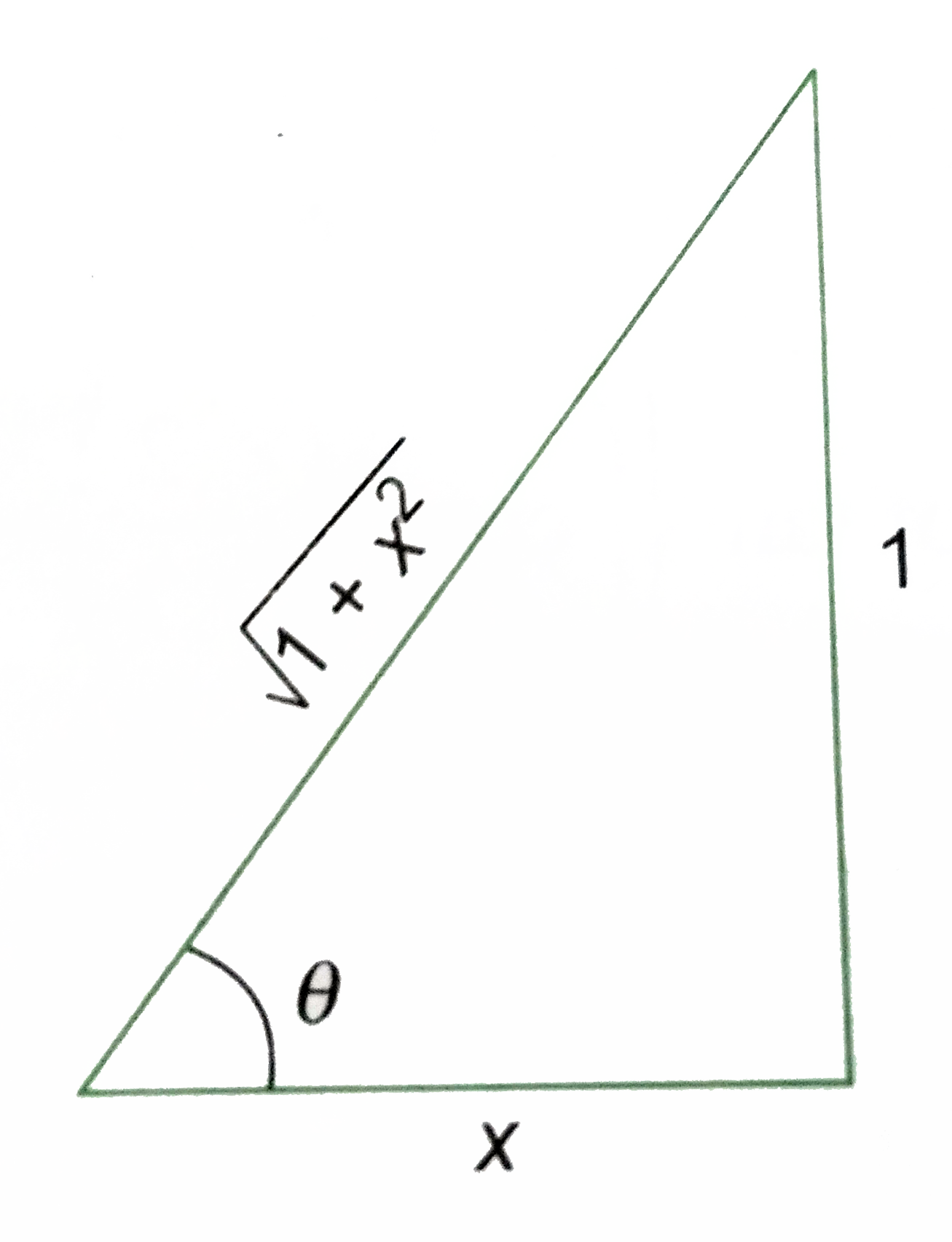
∴E=cos[tan−1(sin(sin−1.1√1+x2)] if x>0
or E=cos[tan−1(sin(π−sin−1.1√1+x2))] if x<0
In each case, E=cos[tan−1(1)√1+x2]
∴E=cos[cos−1√1+x22+x2]
=√x2+1x2+2

|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.112videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise 7.26videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - JEE Previous Year20videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
Similar Questions
Prove that cos⎡⎣tan−1⎧⎨⎩(sin(cot−1x}]=(x2+1x2+2)12
View SolutionProve that cos[tan−1{sin(cos−1x)}]=1√2−x2
View SolutionProve that : sincot−1tancos−1x=x
View SolutionProve the following: cos{tan−1{sin(cot−1x)}}= √1+x22+x2
View SolutionProve that tan−1x+cot−1(x+1)=tan−1(x2+x+1).
View SolutionProve that : tan−1x+cot−1(1+x)=tan−1(1+x+x2)
View SolutionProve that: sin[cot−1{cos(tan−1x)}]=√x2+1x2+2cos[tan^(-1){sin(cot−1x)}]=√x2+1x2+2
View SolutionProve that sin[2tan−1{√1−x1+x}]=√1−x2
View SolutionProve that : 2tan−1(cosectan−1x−tancot−1x)=tan−1x
View SolutionProve thatsin−1x=cos−1√1−x2
View Solution

