Prove that costan−1sincot−1x=√x2+1x2+2Solution in Bengali
E=cos(tan−1(sin(cot−1x)))
Let cot−1x=θ
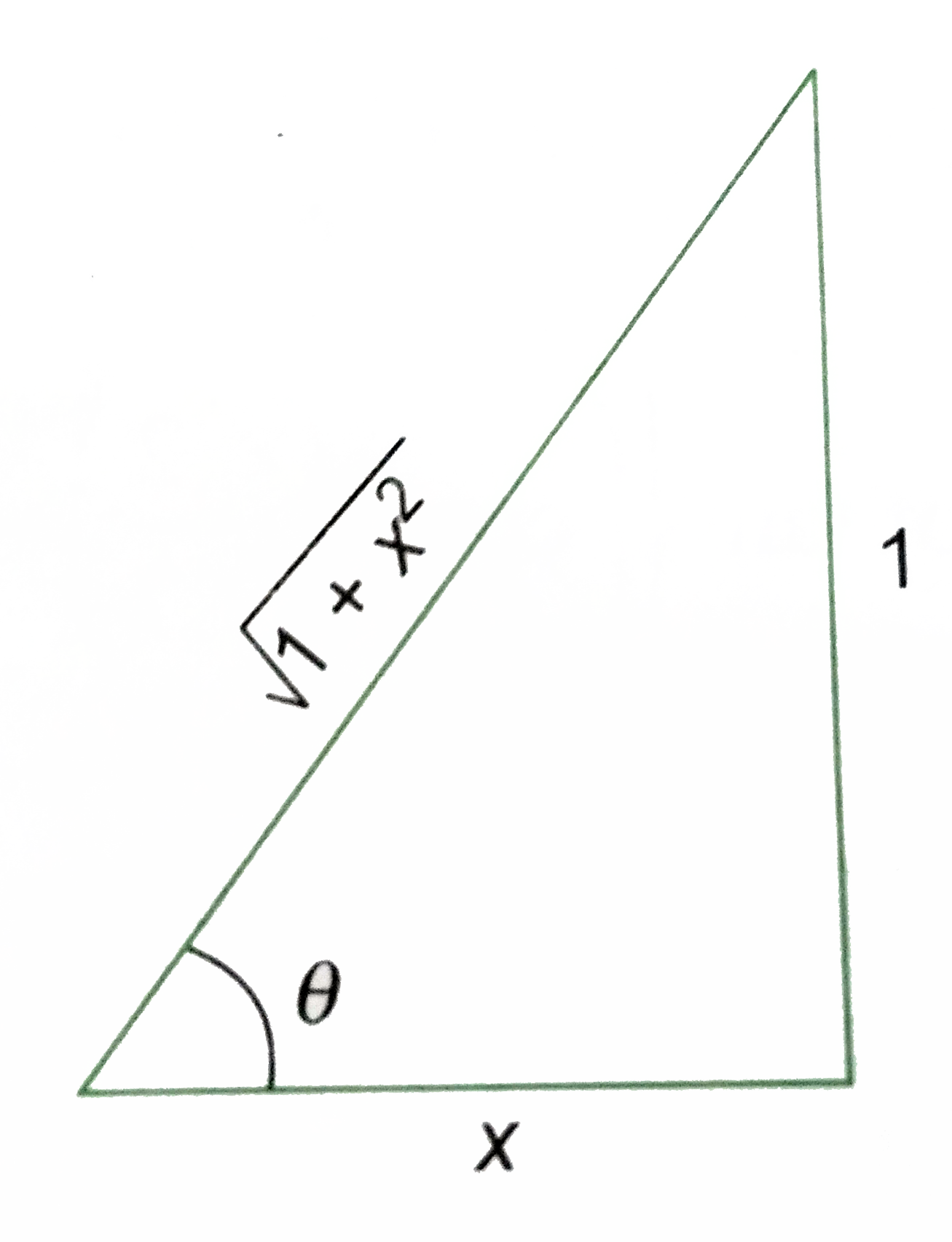
∴E=cos[tan−1(sin(sin−1.1√1+x2)] if x>0
or E=cos[tan−1(sin(π−sin−1.1√1+x2))] if x<0
In each case, E=cos[tan−1(1)√1+x2]
∴E=cos[cos−1√1+x22+x2]
=√x2+1x2+2

Topper's Solved these Questions
Similar Questions
The points with position vectors →x+→y,→x−→yand→x+λ→y are collinear for all real values of λ.
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View Solutionसिद्ध कीजिए कि
tan−1(√1+x2+√1−x2√1+x2−√1−x2)=π4+12cos−1x2
View Solutionसिद्ध करे कि
sincot−1tancos−1x=x.
View Solutionसिद्ध करे कि
costan−1sincot−1x=√x2+1x2+2
View Solutionसिद्ध कीजिए कि :
∫1−1(√1+x+x2−√1−x+x2)dx=0
View SolutionProve that :
tan−1(√1+x2+√1−x2√1+x2−√1−x2)=π4+12cos−1x2
View Solutionপ্রমাণ করো যে, costan−1sincot−1x=(x2+1x2+2)12
View Solutionপ্রমাণ করো:sincot−1cos(tan−1x)=√x2+1x2+2(x>0)
View SolutionProve that tan−1[√1+x2+√1−x2√1+x2−√1−x2]=π4+12cos−1x2
View SolutionProve that costan−1sincot−1x=√x2+1x2+2
View SolutionProve that :
tan−1(√1+x2+√1−x2√1+x2−√1−x2)=π4+12cos−1x2.
View Solutionf(x)=sin{cot−1(x+1)}−cos(tan−1x),a=costan−1sincot−1x,b=cos(2cos−1x+sin−1x)
If f(x)=0 then a2=
View Solutionf(x)=sin{cot−1(x+1)}−cos(tan−1x),a=costan−1sincot−1x,b=cos(2cos−1x+sin−1x)
If a2=26/51, then b2=
View Solutionsincot−1costan−12=
View SolutionProve that tan−1(√1+x2+√1−x2√1+x2−√1−x2)=π4+12cos−1x2
View Solution
