Prove that $[lim_{x \to 0} \frac{\sin x}{x}] = 0,$ where $[.]$ represents the greatest integer function.

Video Solution

Text Solution

Verified by Experts

See the graphs of y=x and $\sin x$ in the following figure.

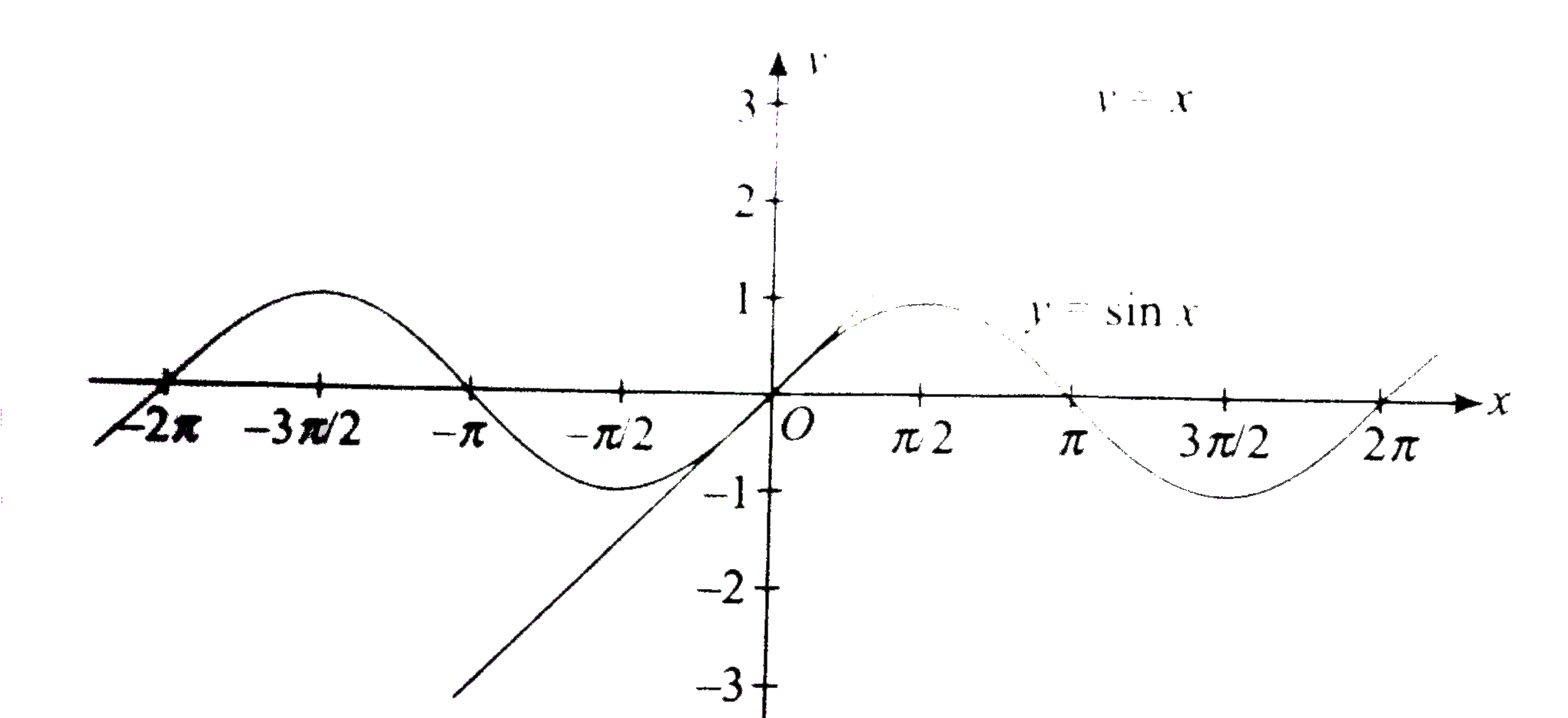
From the figure when $x \to 0^{+}$ ,graph of y=x is above the graph of $y = \sin x$
i.e., $\sin x < x or \frac{\sin x}{x} < 1$
$\Rightarrow lim_{x \to 0^{+}} \frac{\sin x}{x} = 1^{1 -}$
$\Rightarrow [lim_{x \to 0^{+}} \frac{\sin x}{x}] = 0$
When $x \to 0^{-}$ , graph of y=x is below the graph of $y = \sin x$
i.e., $\sin x < x or \frac{\sin x}{x} < 1$ (as x is negative)
$\Rightarrow lim_{x \to 0^{-}} \frac{\sin x}{x} = 1^{-}$
$\Rightarrow [lim_{x \to 0^{-}} \frac{\sin x}{x}] = 0$
Thus, $[lim_{x \to 0^{-}} \frac{\sin x}{x}] = 0$

|

Updated on:21/07/2023

Class 12 MATHS LIMITS AND DERIVATIVES

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-LIMITS-Comprehension Type

Home
Ask Doubt
Profile