Evalute [limx→0sin−1xx]=1, where[⋅] represets the greatest interger function.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

See the graphs of y=x and y=sin−1x in the following figure.
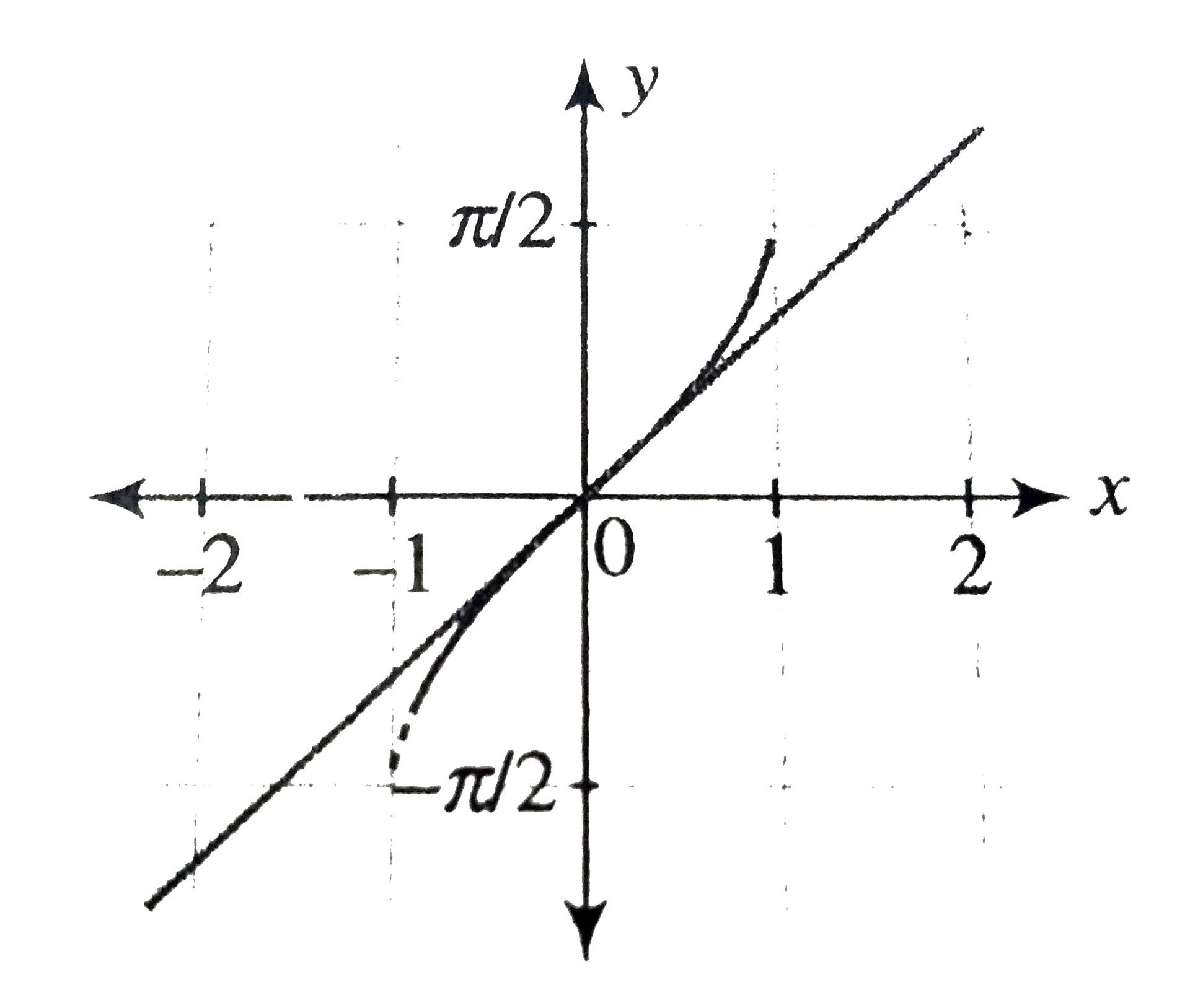
ocr_image
For f(x)=sin−1x∴f'(x)=1√1−x2
f'(0)=1
So the curvetouches the line y=x at x=0.
For 0<x<1,f'(x)>1
So the graph of y sin−1x lies above the graph of y=x.
From the graph, when x→0+, the graph of y=sin−1 is above the graph of y=x
or sin−1x>x⇒sin−1xx>1⇒[limx→0+sin−1xx]=1
When x→0−, the graph of y=sin−1x is below the graph of y = x
or sin−1x<x⇒sin−1xx>1(as x is negative)⇒[limx→0+sin−1xx]=1
Thus, [limx→0+sin−1xx]=1

Updated on:21/07/2023
|