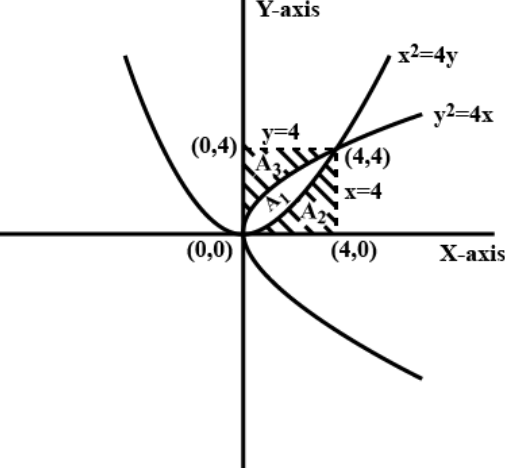
Prove that the curves $y^{2} = 4 x$ and $x^{2} = 4 y$ divide the area of the square bounded by $x = 0, x = 4, y = 4 a n d y = 0$ into three equal parts.

Video Solution

Text Solution

Verified by Experts

To prove
$A_{1} = A_{2} = A_{3} = \frac{A}{3}$ [ A= area of square]
$A = 4 \times 4 = 16$ sq. units
$A_{1} = \int_{0}^{4} \frac{x^{2}}{4} d x = \frac{16}{3}$ sq.units
$A_{2} = \int_{0}^{4} \frac{y^{2}}{4} d y = \frac{16}{3}$
$A_{3} = A - (A_{1} - A_{2})$
$= 16 - 2 \times \frac{16}{3}$
$= \frac{16}{3}$ sq.units
Hence proved
$A_{1} = A_{2} = A_{3} = \frac{A}{3}$

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The area of the region bounded by $y = x^{2}$ and y = 4x , for x between 0 and 1 is equal to
A2 sq. units
B $\frac{5}{3}$ sq. units
C6 sq. units
D1 sq. units
Question 2 - Select One
Find the area of the region bounded by the curve $y^{2} = 4 x and x^{2} = 4 y$ .
A $\frac{15}{7} sq units$
B $\frac{16}{7} sq units$
C $\frac{16}{3} sq units$
D $16 sq units$

NCERT-APPLICATION OF INTEGRALS-SOLVED EXAMPLES

Home
Ask Doubt
Profile