prove that the line joining the mid-point of two equal chords of a circle subtends equal angles with the chord.
Given Two equal chords AB and CD of a circle C(O,r) which have E and F as their midpoints respectively.
To Prove , and
.
Construction Join OE and OF
Proof We know that the line joining the centre of a circle to the midpoint of a chord is perpendicular to the chord.
and .
Now, since AB and CD are equal chords, they must be equidistant from the centre.
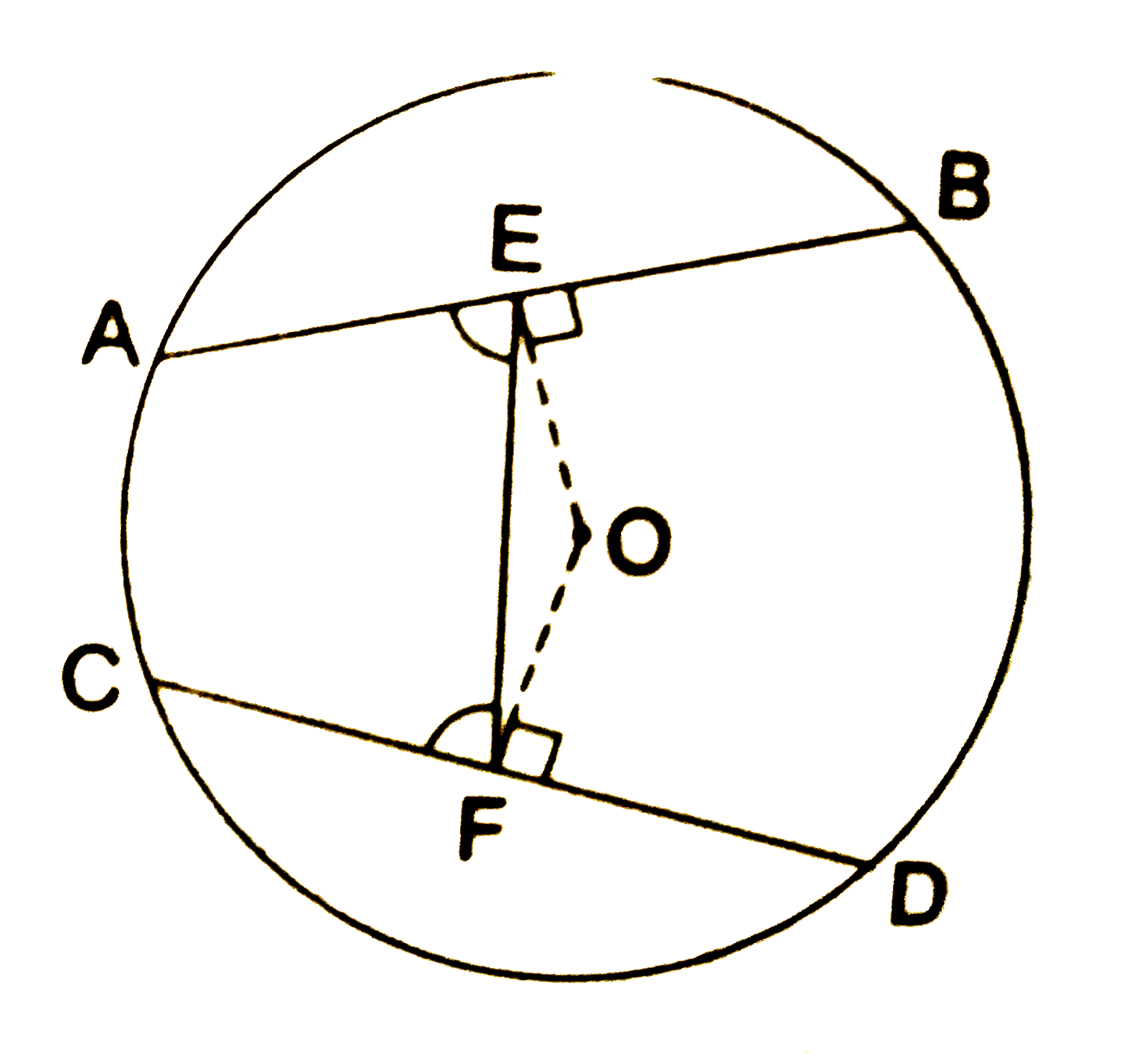
Now, in , we have
and
and .
Similar Questions
Equal chords of a circle subtend equal angles at the centre.
View SolutionProve that equal chords of a circle subtend equal angles at the centre.
View SolutionEqual chord of circle subtends equal angle on centre.
View SolutionProve that the line joining the mid-points of two parallel chords of a circle passes through the centre.
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionState and prove that :
Theorem 10.1 : Equal chords of a circle subtend equal angles at the centre
View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
View SolutionThe locus of the mid points of all equal
chords in a circle is :
View SolutionProve that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
View Solution
