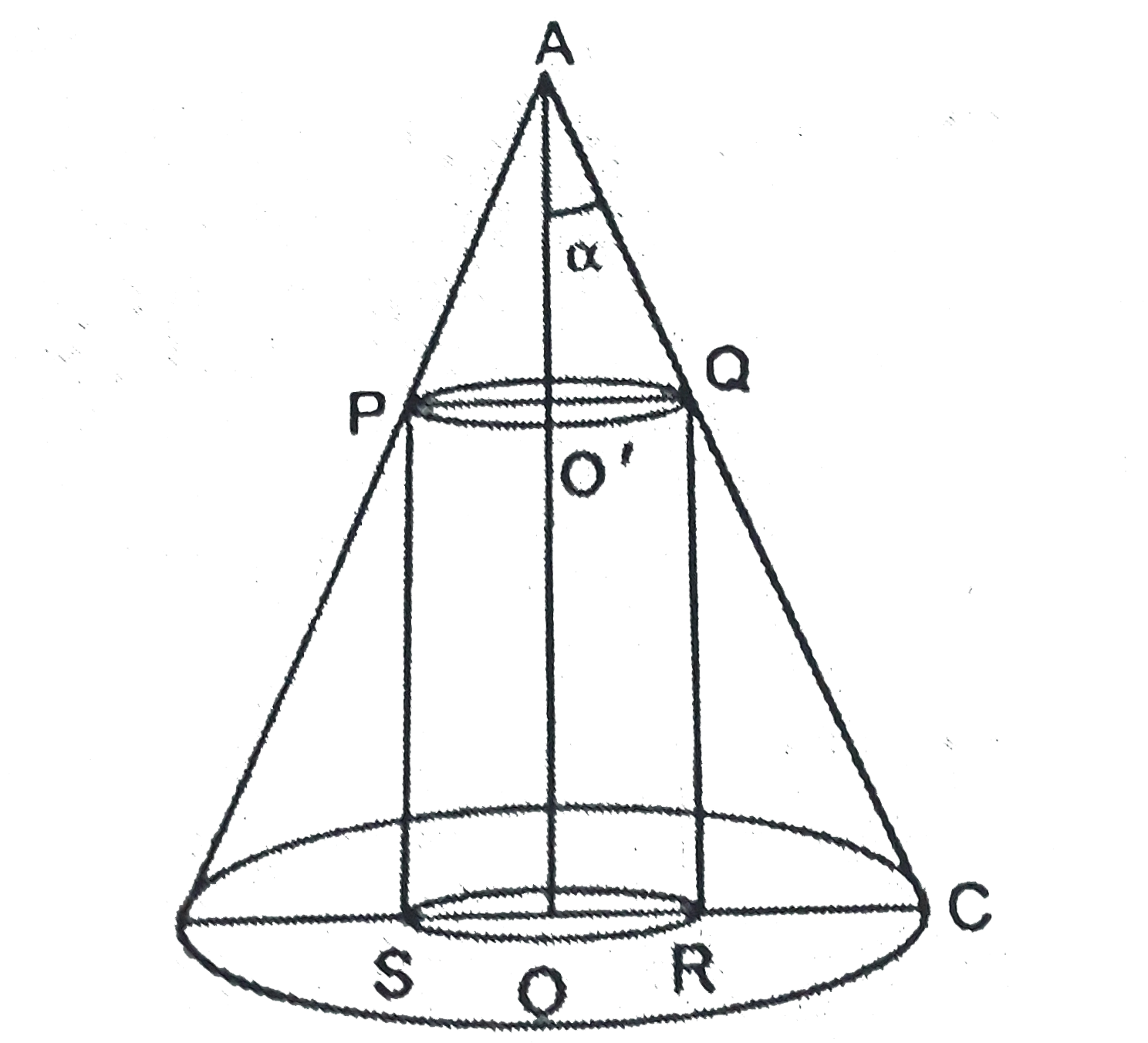
Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.

Video Solution

Text Solution

Verified by Experts

Let the height of cone = h and semivertical angle be $α$ .
Let the radius of cylinder = x.'
Height of cylinder = OO'
=AO - AO'
= $h - x cot α$
$∴$ Curved surface of cylinder
$C = 2 π x \cdot (h - x cot α)$
$= 2 π (h x - x^{2} cot α)$
$\Rightarrow \frac{d C}{d x} = 2 π (h - 2 x cot α)$

For maxima/minima
$\frac{d C}{d x} = 0$
$\Rightarrow h - 2 x cot α = 0$
$\Rightarrow cot α = \frac{h}{2 x}$
$\Rightarrow \frac{h}{r} = \frac{h}{2 x}$
(Where 'r' = radius of the cone)
$\Rightarrow x = \frac{r}{2}$
and $\frac{d^{2} C}{{d x}^{2}} = 2 π (0 - 2 cot α) = - 4 π cot α < 0$
$\Rightarrow$ The value of C is maximum.
Hence, the curved surface area of the cylinder will be maximum when $x = r / 2$ i.e., the radius of cylinder will be half of the radius of cone.

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF DERIVATIVES-Miscellaneous Exercise

Home
Ask Doubt
Profile