Prove that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
Let AB be a chord of a circle C(O,r).
Let PQ be the right bisector of a chord AB, intersecting it at L and the circle at P and Q.
Since the right bisector of a chord always pass through the centre of the circle, PQ must pass through O
Join OA and OB.
OA = OB [each equal to r]
∠ALO=∠BLO[ each eqal to 90∘ ]
OL=OL [common]
∴ΔOLA≅ΔOLB
⇒∠AOL=∠BOP
⇒m(ˆAP)=m(ˆBP)
⇒ˆAP≅ˆBP.
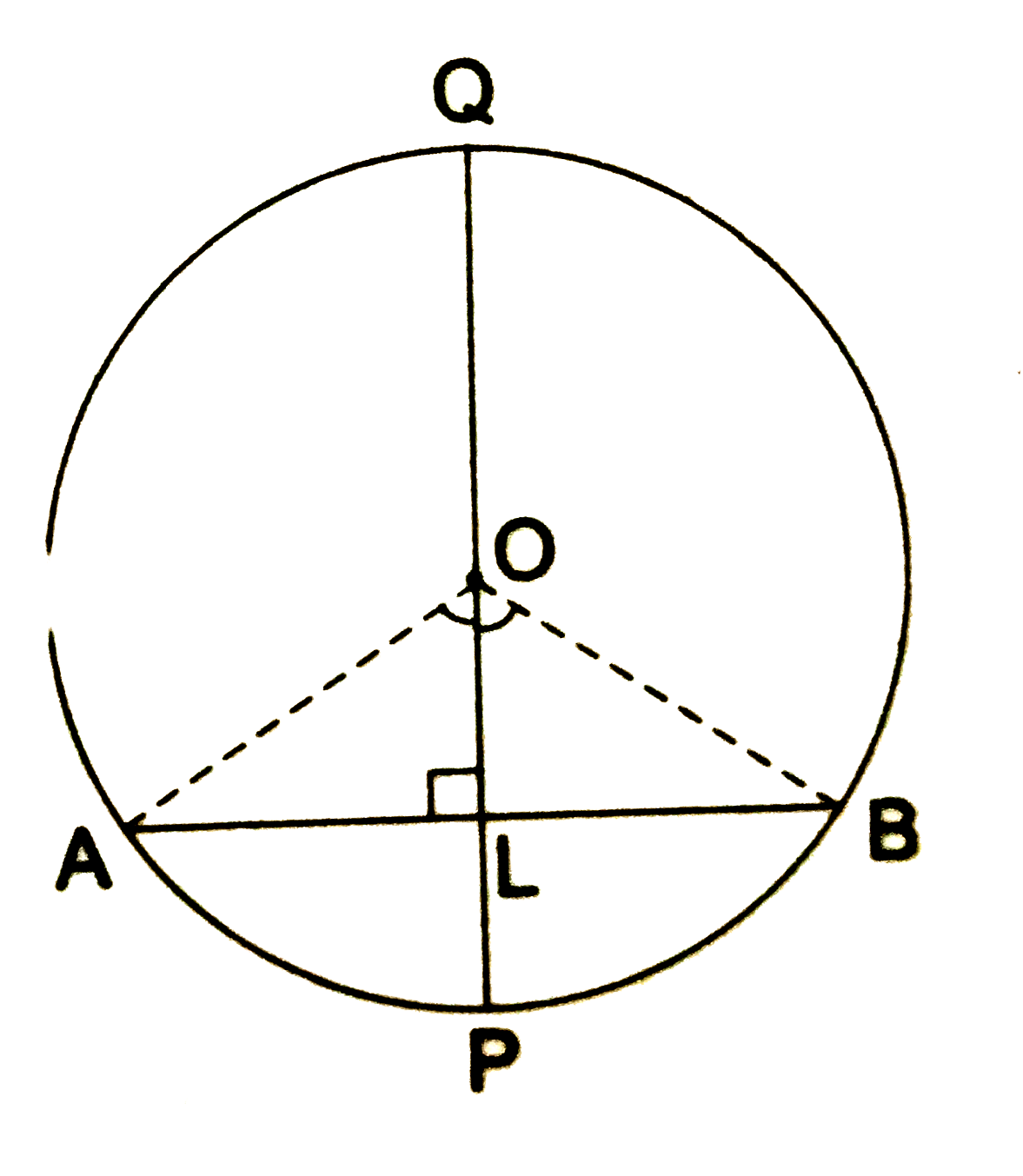
Note the right bisector of a chord also bisects the corresponding major arc.
Similar Questions
Prove that the perpendicular bisector of a chord of a circle always passes through the centre.
View SolutionProve that the diameter is the greatest chord in a circle.
View SolutionIf two arcs of a circle are congruent; then corresponding chords are equal
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf the length of an arc of a circle of radius a is equal to that of an arc of a circle of radius 2a, then the angle of the corresponding sector of the first circle is double the angle of the corresponding sector of the other circle. Is this statement false? Why?
View SolutionIf the length of an arc of a circle of radius r is equal to that of an arc of a circle of radius 2r, then the angle of the corresponding of the other circle. Is this statement false ? Why ?
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionProve that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
View SolutionIf the perpendicular bisector of a chord AB of a circle PXAQBY intersects the circle at P and Q, prove that arc PXA≅arc PYB.

View SolutionTheorem :-2 The perpendicular from centre of a circle to the chord bisects the chord and Perpendicular bisectors of two chords of a circle intersects at the centre.
View Solution
