Prove that the diameter is the greatest chord in a circle.
To prove: AB>CD
Construction: Join OC and OD.
Proof: Let O be the center of the circle ABCD.
Let AB be the diameter and CD be a chord other than diameter of the circle.
OA=OB=OC=OD (Radius of the circle)
Now In △OCD,
OC+OD>CD
OA>OB>CD
⇒AB>CD<br>therefore AC>CD
Hence proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The equation of the circle whose diameter is common chord to the circles
Ax2+y2−2ab2a2+b2x+2a2ba2+b2y+c=0Bx2+y2−2ab2a2+b2x+2a2ba2+b2y+c=0Cx2+y2+2ab2a2+b2x+2a2ba2+b2y+c=0Dx2+y2+2ab2a2+b2x−2a2ba2+b2y+c=0
Prove that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View SolutionProve that the circle described on the focal chord as a diameter touches the directrix
View SolutionProve that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
View SolutionFill in the blanks: The diameter of a circle is … times its radius The diameter of a circle is the … chord of the circle. The diameter of a circle pass through…. A chord of a circle is a line segment with its end points on the … If we join any two points on a circle by a line segment, we obtain… A radius of a circle is a line segment with one end at …. and the other end at…. All radii of a circle are… The diameters of circle are… The total number of diameters of circle is… Every point on a circle is…from its centre.. A chord of a circle contains exactly….points of the circle.. A diameter is the longest… Concentric circles are circle having….
View SolutionDetermine equation of the circle whose diameter is the chord x+y=1 of the circle x2+y2= 4
View SolutionProve that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
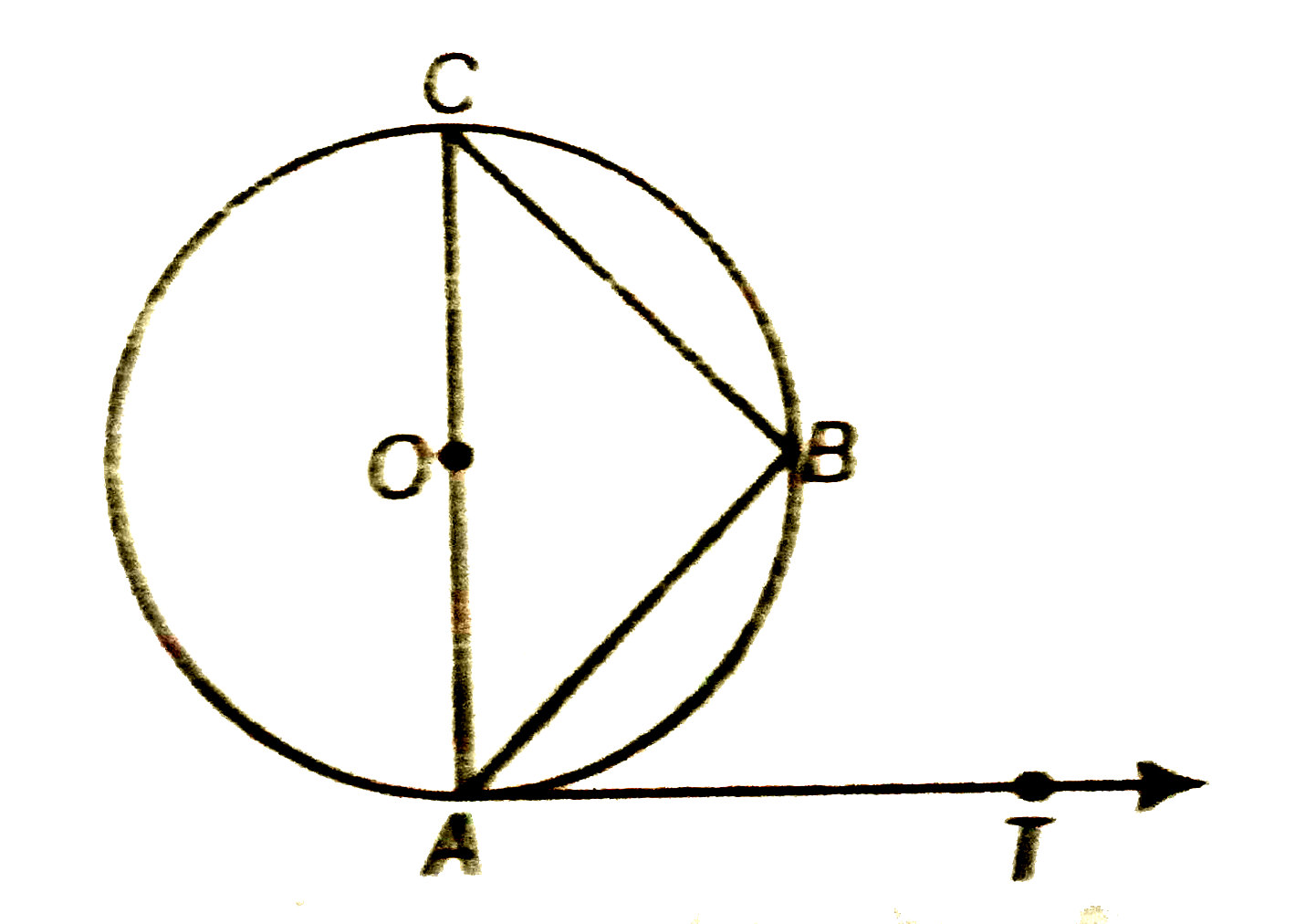
View SolutionIf AB is chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT=∠ACB.
View Solution
