Refers to question 13. Solve the liner progamming problem and deterimine profit to the manufacturer.
The correct Answer is:N/a
Referring to solution 13, we have
Maximise Z=100x+170y subject to 3x+2y le 3600, x+y ge 1800 x ge0, y=180

Hence the maximum profit to the manufacturer is 138600.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - OBJECTIVE
8 Videos
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - FILLERS
7 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Fillers
18 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
Similar Questions
A factory uses three different resources for the manufacture of two different productoof the resource A,12 units of Band16 unit of C being available. One unit of there quires 2,2and4 units of the respective resources and one unit of the second requires 4,2and0 units of respective resources. It is known that the first product givesatof 2 monetary units per unit and the second 3. Formulate the linear programming problem How many units of each product should be manufactured for maximizing the profit? solve it graphically.
View SolutionRefers to question 11. How many of circuit of type A and of type B, should be produced by the manufacture, so as to maximise hi profit? Determine the profit.
View Solution
Knowledge Check
Maximum profit: An barrels manufacturer can produce up to 300 barrels per day. The profit made from the sale of these barrels can be modelled by the function P(x)=−10x2+3500x−66000 where P(x) is the profit in rupees and x is the number of barrels made and sold.

Based on this model answer the following questions:
What is the maximum profit which can manufacturer earn?ARs 240250BRs 480500CRs 680250DRs 240250Refer the following data table and answer the following question.
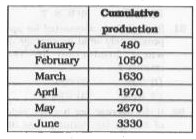
The polygon shows cumulative production of cars manufactured in the month starting from January. How many cars were manufactured in the months of April and May ?AA)1040BB)1360CC)920DD)4640
Refers to question 14. How many sweaters of each type of should the company make in an day to get a maximum profit? What is the maximum profit?
View SolutionFor an objective function Z=ax+by , where a, b > 0; the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
View SolutionSolve the following liner programming problems by graphical method: Maximize Z=50x+30y Subject to 2x+y≤18, 3x+2y≤34 x,y≥0
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of 70 paise and screws B at a profit of Rs 1. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Formulate the above LPP and solve it graphically and determine the maximum profit.
View Solution
