Refers to question 14. How many sweaters of each type of should the company make in an day to get a maximum profit? What is the maximum profit?
The correct Answer is:N/a
Referring to solution 14, 3x+y≤600,x−y≥100,x≥0,y≥0
On solving x+y=300 and 3x+y=600 we get x=150, y=150
On solving x-y=100 and x+y=300 we get x=100, y=200
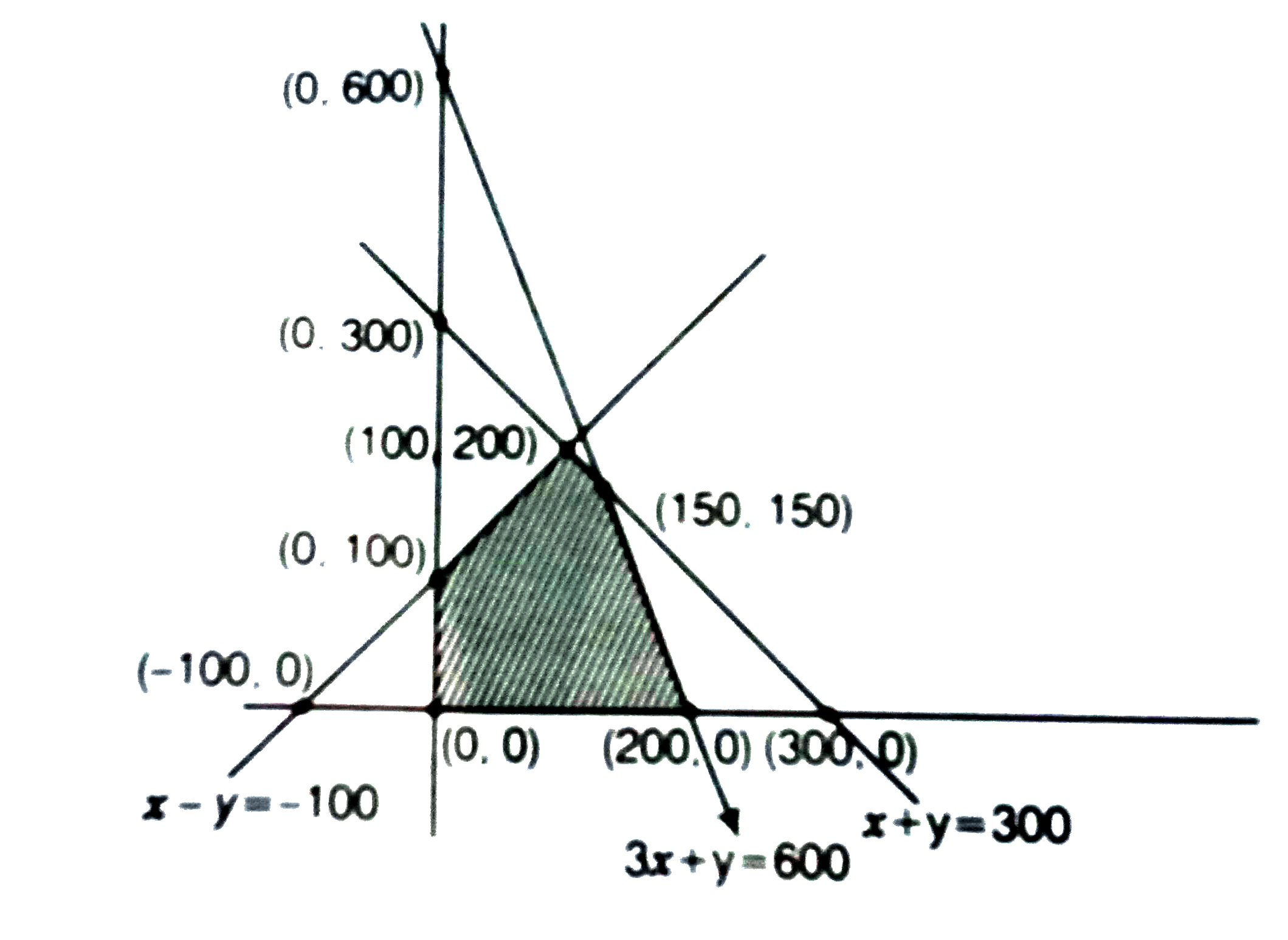
From the shaded feasible region it is clear that corrdingates of corner points are (0,0),(200,0),(150,150),(100,200), and (0,100)

Hence 150 sweaters of each type made by company and maximum profit=48000.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - OBJECTIVE
8 Videos
- LINEAR PROGRAMMINGBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - FILLERS
7 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Fillers
18 Videos
- MATRICESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATRICESEXERCISE - Solved example
101 Videos
Similar Questions
A manufacturing company makes two models A and B of a product. Each piece of mode a requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of Mode B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricati2 and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of Rs. 8000 on each piece of model A and Rs. 12000 on each piece of Model B. How many pieces of Model A and Model B should be manufactured per week to realise a maximum profit? What is the maximum profit per week?
View Solution(Manufacturing problem) A manufacturing company makes two models A and B of a product. Each piece of Model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of Model B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of Rs 8000 on each piece of model A and Rs 12000 on each piece of Model B. How many-pieces of Model A and Model B should be manufactured per week to realise a maximum profit? What is the maximum profit per week?
View Solution
Knowledge Check
(Manufacturing problem) A manufacturing company makes two models A and B of a product. Each piece of Model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of Model B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of Rs 8000 on each piece of model A and Rs 12000 on each piece of Model B. How many-pieces of Model A and Model B should be manufactured per week to realise a maximum profit? What is the maximum profit per week?
A150000B168000C180000D190000
A company manufactures two types of toys A and B. A toy of type A requires 5 minute for cutting and 10 minute for assembling. A toy of type B requires 8 minute for cutting and 8 minutes for assembling. There are 3 hours available for cutting and 4 hours available for assembling th etoys in a day. The profit is Rs 50 each on a toy of Type A and Rs 60 each on a toy of type B. How many toys of each type should the company manufacture in a day to maximize the profit ? Use linear programming to find the solution.
View SolutionA company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. He earns a profit of Rs.50 each on type A and Rs.60 each on type. B. How many toys of each type should the company manufacture in a day to maximize the profit ?
View SolutionA copany manufactures two types of toys, A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs.50 each on type A and Rs.60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
View SolutionA company produces two types of good, A and B, that require gold and silver. Each unit of type A requires 3 gm of silver and 1 gm of gold while that of type B requires 1 gm of silver and 2 gm of gold. The company can produce 9 gm of silver and 8 gm of gold. If each unit of type A brings a profit of Rs. 40 and that of type B Rs. 50, find the number of units of each type that the company should produce to maximize the profit. What is the maximum profit?
View SolutionA man has Rs. 1500 to purchase two types of shares of two different companies s1 and s2. Markedt price of one share of s1 is Rs. 180 and s2 is Rs. 120. He wishes to purchase a maximum of ten shares only. If one share of type s1 gives a yield of Rs. 11 and of type s2 yields Rs. 8 then how much shares of each type must be purchased to get maximum profit? And what will be the maximum profit?
View SolutionA company produces two types of items, and Q. Manufacturing of both items requires the metals gold and copper. Each unit of item P requires 3 gm of gold and 1 gm of copper while that of item Q requires 1 gm of gold and 2 gm of copper. The company has 9 gm of gold and 8 gm of copper in its store. If each unit of item P makes a profit of Rs 50 and each unit of item O makes a profit of 60, determine the number of units of each item that the company should produce to maximize profit. What is the maximum profit?
View SolutionAn aeroplane can carry a maximum of 200 passengers. A profit of Rs 1000 is made on each executive class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?
View Solution
