Represent (i) A∩(B∪C) and (ii) (A∩B)∪C by venn diagram.
The correct Answer is: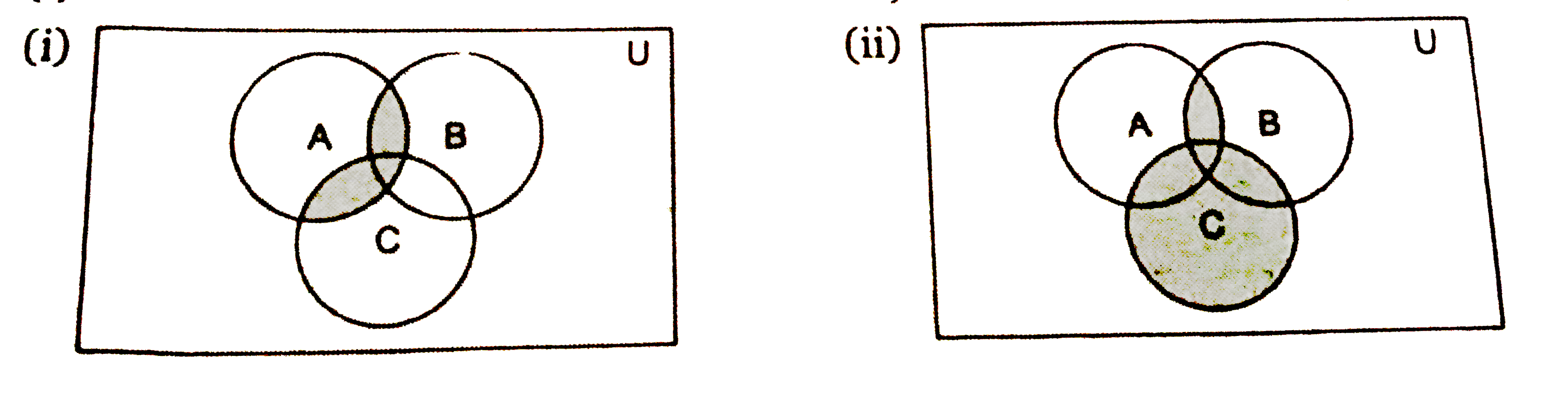
Step by step video & image solution for Represent (i) A cap(BcupC) and (ii) (A capB)cupC by venn diagram. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - Exercise 1E
15 Videos
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - Exercise 1F
12 Videos
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - Exercise 1C
16 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Miscellaneous Exercise
32 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE
7 Videos
Similar Questions
If A={2,3,5,8,10},B={3,4,10,12}andC={4,5,8,14}, then find each of the following :
(i) (A∪B)∩(A∪C)
(ii) (A∩B)∪(A∩C).
View SolutionDraw a Venn-diagram to show the relationship between sets A and B , such that A⊆B. Now shade the region representing :
(i) A∪B, (ii) B'∩A, (iii) A∩B, (iv) (A∪B)'
View SolutionTwo sets A and B are such that A∩B=π. Draw a Venn-diagram to show the relationship between A and B. Shade the region representing :
(i) A∪B, (ii) (A∪B)', (iii) B-A, (iv) B∩A'
View SolutionIf A{1,2,3},B={3,4}andC={4,5,6}, then find the each of the following :
(i) A∩(B∪C)
(ii) (A−B)∪C
(iii) (A∪B)−C
(iv) (A∩B)∪C.
View SolutionGiven A = {0,1, 2,4, 5}, B = {0,2,4, 6, 8} and C = {0, 3, 6, 9}. Show that:
(i) A∪(B∪C)=(A∪B)∪C i.e., the union of the sets is associative.
(ii) A∩(B∩C)=(A∩B)∩C i.e., the intersection of sets is associative.
View SolutionIf A = {1,2,3,4} and B = {6,8,9} , then find A∪B,A∩B and represent these by Venn diagrams .
View SolutionThe diagram represents two inequation A and B on real number lines:
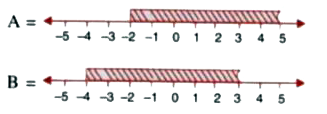
Represent A∩BandA∩B' on two different number lines.
View SolutionFor any two sets A and B, prove that :
(i) (A∩B)∪(A−B)=A
(ii) A∪(B−A)=A∪B.
View SolutionDraw the venn diagram to represent
(i) A∩(B−A)'<br>(ii)A∪B(B∩A)'
View SolutionFor any two sets A and B, prove that :
(i) A−(A−B)=A∩B
(ii) A∩(A'∪B)=A∩B.
View Solution
