Draw the venn diagram to represent
(i) A∩(B−A)'<br>(ii)A∪B(B∩A)'
To solve the given question, we need to draw Venn diagrams for two parts: (i) A∩(B−A) and (ii) A∪B∩(B∩A)′. Let's break down each part step by step.
Part (i): Draw the Venn Diagram for A∩(B−A)
1. Understand the Components:
- A is a set.
- B−A is the set of elements that are in B but not in A.
2. Find B−A:
- This can be represented as the area of set B that does not overlap with set A.
3. Find A∩(B−A):
- This represents the intersection of set A with the elements of set B that are not in A.
- Since there are no elements that can be both in A and in B−A (by definition of B−A), this intersection is empty.
4. Draw the Venn Diagram:
- Draw two overlapping circles representing sets A and B.
- Shade the area representing A∩(B−A), which will be empty.
Part (ii): Draw the Venn Diagram for A∪B∩(B∩A)′
1. Understand the Components:
- A∪B is the union of sets A and B.
- (B∩A)′ is the complement of the intersection of A and B, meaning it includes everything outside of the intersection.
2. Find B∩A:
- This is the area where sets A and B overlap.
3. Find (B∩A)′:
- This includes all elements in the universal set U that are not in the intersection of A and B.
4. Find A∪B∩(B∩A)′:
- This represents the union of sets A and B with the area outside the intersection of A and B.
- Since A∪B covers all elements in both sets, the intersection with (B∩A)′ will include all elements in A and B that are not in their intersection.
5. Draw the Venn Diagram:
- Draw two overlapping circles for sets A and B.
- Shade the entire area of A and B except for the intersection area.
Final Venn Diagrams
- For part (i), the shaded area is empty.
- For part (ii), the shaded area includes all of A and B except the intersection.
- A is a set.
- B−A is the set of elements that are in B but not in A.
- This can be represented as the area of set B that does not overlap with set A.
- This represents the intersection of set A with the elements of set B that are not in A.
- Since there are no elements that can be both in A and in B−A (by definition of B−A), this intersection is empty.
- Draw two overlapping circles representing sets A and B.
- Shade the area representing A∩(B−A), which will be empty.
- A∪B is the union of sets A and B.
- (B∩A)′ is the complement of the intersection of A and B, meaning it includes everything outside of the intersection.
- This is the area where sets A and B overlap.
- This includes all elements in the universal set U that are not in the intersection of A and B.
- This represents the union of sets A and B with the area outside the intersection of A and B.
- Since A∪B covers all elements in both sets, the intersection with (B∩A)′ will include all elements in A and B that are not in their intersection.
- Draw two overlapping circles for sets A and B.
- Shade the entire area of A and B except for the intersection area.
- For part (i), the shaded area is empty.
- For part (ii), the shaded area includes all of A and B except the intersection.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-A(Objective Type Questions (One option is correct))41videos
SETS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-B(Objective Type Question(One option is correct))13videos
SETS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - EXAMPLE24videos
SETS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - J) Aakash Challengers11videos
SEQUENCES AND SERIES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STATISTICSEXERCISE - Section-C Assertion-Reason15videos
STATISTICS
Similar Questions
Use Venn-diagrams to prove that: (A∩B)'=A'∪B'
View SolutionDraw a Venn-diagram to show the relationship between two overlapping sets A and B. Now shade the region representing :
(i) A∩B, (ii) A∪B, (iii) B-AView SolutionFrom the given diagram, find:
(i) (A∪B)−C
(ii) B−(A∩C)
(iii) (B∩C)∪A
Verify: A−(B∩C)=(A−B)∪(A−C)
 View Solution
View SolutionFrom the given diagram, find:
(i) A', (ii) B', (iii) A'∪B', (iv) (A∩B)'
Is A'∪B'=(A∩B)' ?
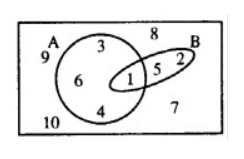 View Solution
View SolutionFrom the given diagram find:
(i) A∪B
(ii) A'∩B
(iii) A-B
(iv) B-A
(v) (A∪B)'
 View Solution
View SolutionTwo sets A and B are such that A∩B=π. Draw a Venn-diagram to show the relationship between A and B. Shade the region representing :
(i) A∪B, (ii) (A∪B)', (iii) B-A, (iv) B∩A'View SolutionDraw a Venn-diagram to show the relationship between sets A and B , such that A⊆B. Now shade the region representing :
(i) A∪B, (ii) B'∩A, (iii) A∩B, (iv) (A∪B)'View SolutionUse the given diagram to find:
(i) A∪(B∩C)
(ii) B−(A−C)
(iii) A-B
(iv) A∩B'
is A∩B'=A−B?
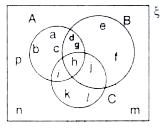 View Solution
View Solution(i) Draw Venn diagram to represent A∩(B∪C) (ii) If A={1,2,3,4}. B={3,4,6,7}, C={1,3,7}, U={1,2,3…..10} then represent the given data by a Venn diagram.
View SolutionProve (A∩B)'=(A'∪B')
View Solution

