RICE is a rhombus (Fig 3.36). Find x, y, z. Justify your findings.
To solve the problem, we need to find the values of x, y, and z in the rhombus RICE. Here’s a step-by-step solution:
Step 1: Understand the Properties of a Rhombus
A rhombus has the following properties:
- All sides are equal.
- The diagonals bisect each other at right angles (90 degrees).
Step 2: Identify the Values of x and y
Given that RICE is a rhombus:
- Let EO and OI be the two halves of one diagonal. Since the diagonals bisect each other, we have:
- EO = OI = x
- Since EO = 5 cm, we can conclude that:
x=5cm
- Now, let CR be the other diagonal. Since OC and OR are the two halves of this diagonal:
- OC = 12 cm, therefore:
y=12cm
Step 3: Use Pythagoras Theorem to Find z
In triangle OIR, which is a right triangle:
- We can apply the Pythagorean theorem, which states:
Hypotenuse2=Perpendicular2+Base2
- Here, IR is the hypotenuse (which we are calling z), IO is the perpendicular (which is x), and OR is the base (which is y):
z2=IO2+OR2
z2=x2+y2
z2=52+122
z2=25+144
z2=169
Step 4: Calculate z
Now, we take the square root of both sides:
z=√169
z=13cm
Summary of Findings
- x=5cm
- y=12cm
- z=13cm
Justification
- The values of x and y were determined based on the properties of the rhombus, specifically that the diagonals bisect each other.
- The value of z was calculated using the Pythagorean theorem in the right triangle formed by the diagonals.
A rhombus has the following properties:
- All sides are equal.
- The diagonals bisect each other at right angles (90 degrees).
Given that RICE is a rhombus:
- Let EO and OI be the two halves of one diagonal. Since the diagonals bisect each other, we have:
- EO = OI = x
- Since EO = 5 cm, we can conclude that:
x=5cm
- OC = 12 cm, therefore:
y=12cm
In triangle OIR, which is a right triangle:
- We can apply the Pythagorean theorem, which states:
Hypotenuse2=Perpendicular2+Base2
- Here, IR is the hypotenuse (which we are calling z), IO is the perpendicular (which is x), and OR is the base (which is y):
z2=IO2+OR2
z2=x2+y2
z2=52+122
z2=25+144
z2=169
Now, we take the square root of both sides:
z=√169
z=13cm
- x=5cm
- y=12cm
- z=13cm
- The values of x and y were determined based on the properties of the rhombus, specifically that the diagonals bisect each other.
- The value of z was calculated using the Pythagorean theorem in the right triangle formed by the diagonals.
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.26videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.311videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.311videos
UNDERSTANDING QUADRILATERALS
- BOOK - NCERT ENGLISHCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.49videos
SQUARES AND SQUARE ROOTS
- BOOK - NCERT ENGLISHCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.38videos
VISUALISING SOLID SHAPES
Similar Questions
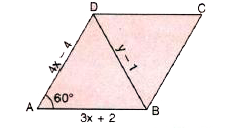
The given figure shows a rhombus ABCD. Find x and y
 View Solution
View SolutionThe diagonals of a quadrilateral are perpendicular to each other. Is such a quadrilateral always a rhombus? If your answer is ‘No’, draw a figure to justify your answer.
View Solution(a) Find x+y+z (b) Find x+y+z+w
View SolutionTwo sides of a rhombus lying in the first quadrant are given by 3x−4y=0 and 12x−5y=0. If the length of the longer diagonal is 12, then find the equations of the other two sides of the rhombus.
View SolutionIn figure, find x+y+z.
 View Solution
View SolutionFor what value of x + y in figure will ABC be a line? Justify your answer.
View SolutionIf the two sides of rhombus are x+2y+2=0 and 2x+y−3=0, then find the slope of the longer diagonal.
View SolutionIf the two sides of rhombus are x+2y+2=0 and 2x+y−3=0, then find the slope of the longer diagonal.
View SolutionFind out whether the following sentence is a statement or not. Justify your answer: Every rhombus is a square.
View SolutionFind out whether the following sentence is a statement or not. Justify your answer: Go!
View Solution


