RENT is a rectangle (Fig 3.41). Its diagonals meet at O. Find x, if OR=2x+4andOT=3x+1
To solve the problem, we need to find the value of x given that in rectangle RENT, the diagonals intersect at point O, and we have the lengths OR=2x+4 and OT=3x+1.
1. Understanding the Properties of a Rectangle:
In a rectangle, the diagonals bisect each other. This means that OR=ON and OT=OE.
2. Setting Up the Equations:
Since OR=ON and OT=OE, we can write:
OR=2x+4
OT=3x+1
3. Using the Bisecting Property:
Since R and T are opposite corners of the rectangle, the lengths of the diagonals must be equal:
RN=TE
This means:
2×OR=2×OT
4. Substituting the Values:
Substitute the expressions for OR and OT into the equation:
2(2x+4)=2(3x+1)
5. Simplifying the Equation:
Expanding both sides:
4x+8=6x+2
6. Rearranging the Equation:
Move all terms involving x to one side and constant terms to the other side:
4x−6x=2−8
This simplifies to:
−2x=−6
7. Solving for x:
Divide both sides by -2:
x=−6−2=3
Final Answer:
The value of x is 3.
---
In a rectangle, the diagonals bisect each other. This means that OR=ON and OT=OE.
Since OR=ON and OT=OE, we can write:
OR=2x+4
OT=3x+1
Since R and T are opposite corners of the rectangle, the lengths of the diagonals must be equal:
RN=TE
This means:
2×OR=2×OT
Substitute the expressions for OR and OT into the equation:
2(2x+4)=2(3x+1)
Expanding both sides:
4x+8=6x+2
Move all terms involving x to one side and constant terms to the other side:
4x−6x=2−8
This simplifies to:
−2x=−6
Divide both sides by -2:
x=−6−2=3
The value of x is 3.
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.2
6 Videos
- UNDERSTANDING QUADRILATERALSBOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.3
11 Videos
- UNDERSTANDING QUADRILATERALSBOOK - NCERT ENGLISHCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.3
11 Videos
- SQUARES AND SQUARE ROOTSBOOK - NCERT ENGLISHCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.4
9 Videos
- VISUALISING SOLID SHAPESBOOK - NCERT ENGLISHCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.3
8 Videos
Similar Questions
The figure, RENT is a rectangle. Its diagonals meet at O. Find x, if OR=2x+4 and OT=3x+1.
View Solution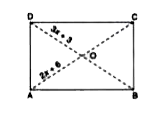
In the given figure, the diagonals AC and BD of a rectangle ABCD intersect each other at point O.
If OA=2x+6 and OD=3x+3, find the value of x.
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=440, find ∠OAD
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=440, find ∠OAD.
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=440, find ∠OAD.
View SolutionThe equation of one side of a rectangle is 3x−4y−10=0 and the coordinates of two of its vertices are (−2,1)and(2,4). Find the area of the rectangle and the equation of that diagonal of the rectangle which passes through the point (2,4).
View SolutionTwo sides of a parallelogram are along the lines x+y=3 and x=y+3. If its diagonals intersect at (2, 4) , then one of its vertices is
View SolutionFind the equations of the circles drawn on the diagonals of the rectangle as its diameter whose sides are x=5, x=−2, y=3 and y=−1.
View SolutionThe equation of one side of a rectangle is 3x−4y−10=0 and the coordinates of two of its vertices are (−2,1)and(2,4). Then, the area of the rectangle is
View SolutionThe sides of a rectangle are given by the equations x=-2, x = 4, y=-2 andy=5. Find the equation of the circle drawn on the diagonal of this rectangle as its diameter.
View Solution
