rr1r2r3=
R2
S2
s2
none
The correct Answer is:B
To solve the problem r⋅r1⋅r2⋅r3, where r is the radius of the incircle and r1,r2,r3 are the radii of the excircles of a triangle, we can follow these steps:
Step 1: Understand the Definitions
- Let r be the radius of the incircle of triangle ABC.
- Let r1,r2,r3 be the radii of the excircles opposite to vertices A,B,C respectively.
Step 2: Use the Formulas
The formulas for the inradius r and the exradii r1,r2,r3 are:
- r=As
- r1=As−a
- r2=As−b
- r3=As−c
Where:
- A is the area of the triangle.
- s is the semi-perimeter of the triangle, given by s=a+b+c2.
Step 3: Substitute the Values
Now, substituting the values into the expression r⋅r1⋅r2⋅r3:
r⋅r1⋅r2⋅r3=(As)⋅(As−a)⋅(As−b)⋅(As−c)
Step 4: Combine the Terms
This can be simplified as:
r⋅r1⋅r2⋅r3=A4s⋅(s−a)⋅(s−b)⋅(s−c)
Step 5: Use Heron's Formula
Using Heron's formula for the area A:
A=√s(s−a)(s−b)(s−c)
Substituting this into the equation gives:
A2=s(s−a)(s−b)(s−c)
Thus:
A4=(s(s−a)(s−b)(s−c))2
Step 6: Final Expression
Now substituting back into our expression:
r⋅r1⋅r2⋅r3=(s(s−a)(s−b)(s−c))2s⋅(s−a)(s−b)(s−c)
This simplifies to:
r⋅r1⋅r2⋅r3=s⋅(s−a)(s−b)(s−c)
Conclusion
Thus, the final result is:
r⋅r1⋅r2⋅r3=s⋅(s−a)(s−b)(s−c)
- Let r be the radius of the incircle of triangle ABC.
- Let r1,r2,r3 be the radii of the excircles opposite to vertices A,B,C respectively.
The formulas for the inradius r and the exradii r1,r2,r3 are:
- r=As
- r1=As−a
- r2=As−b
- r3=As−c
- A is the area of the triangle.
- s is the semi-perimeter of the triangle, given by s=a+b+c2.
Now, substituting the values into the expression r⋅r1⋅r2⋅r3:
r⋅r1⋅r2⋅r3=(As)⋅(As−a)⋅(As−b)⋅(As−c)
This can be simplified as:
r⋅r1⋅r2⋅r3=A4s⋅(s−a)⋅(s−b)⋅(s−c)
Using Heron's formula for the area A:
A=√s(s−a)(s−b)(s−c)
Substituting this into the equation gives:
A2=s(s−a)(s−b)(s−c)
Thus:
A4=(s(s−a)(s−b)(s−c))2
Now substituting back into our expression:
r⋅r1⋅r2⋅r3=(s(s−a)(s−b)(s−c))2s⋅(s−a)(s−b)(s−c)
This simplifies to:
r⋅r1⋅r2⋅r3=s⋅(s−a)(s−b)(s−c)
Thus, the final result is:
r⋅r1⋅r2⋅r3=s⋅(s−a)(s−b)(s−c)
Topper's Solved these Questions
- PROPERTIES OF TRIANGLES BOOK - ML KHANNACHAPTER - PROPERTIES OF TRIANGLES EXERCISE - Problem Set (4)(TRUE AND FALSE)
9 Videos
- PROPERTIES OF TRIANGLES BOOK - ML KHANNACHAPTER - PROPERTIES OF TRIANGLES EXERCISE - Problem Set (4)(FILL IN THE BLANKS)
3 Videos
- PROPERTIES OF TRIANGLES BOOK - ML KHANNACHAPTER - PROPERTIES OF TRIANGLES EXERCISE - Problem Set (3)(FILL IN THE BLANKS)
2 Videos
- PROGRESSIONS BOOK - ML KHANNACHAPTER - PROGRESSIONS EXERCISE - MISCELLANEOUS EXERCISE (ASSERTION/REASON)
1 Video
- RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINEBOOK - ML KHANNACHAPTER - RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINEEXERCISE - COMPREHENSION
11 Videos
Similar Questions
Prove the questions
a(rr1+r2r3)=b(rr2+r3r1)=c(rr3+r1r2)
View SolutionThree circles of radii r1,r2andr3 are drawn concentric to each other. The radii r1 and r2 are such that the area of the circle with radius r1 is equal to the area between the circle of radius r2 and r1 . The area between the circle of radii r2 and r3 is equal to area between the circle of radii r2 and rr . What is the value of r1:r2:r3 ?
View Solution
Knowledge Check
r1+r2+r3−r=
ARB2RC3RD4RIf r,r1,r2,r3 have their usual meanings , the value of 1r1+1r2+1r3, is
A1B0C1rDnone of theseFor a cubic poltnomial a3x3+a2x2+a1x+a0 the roots r1,r2,r3 come in three symmetric combinations: C1=r1+r2+r3,C2=r1r2+r2r3+r3r1,C3=r1r2r3 The sum of the kth powers of the roots is defined as Sk=rk1+rk2+rk3 Then
a3S1+a2=0
a3S2+a2S1+2a1=0Aonly (i) is trueBonly (ii) is trueCboth are trueDnone are true
r2r3+r3r1+r1r2=S2/r2, true or false?
View SolutionThere circle C1,C2 and C3 with radii r1,r2 and r3 (where r1<r2<r3) are placed as shown in the given figure. What is the value of r2?
तीन वृत्तC1,C2 तथा C3 जिनको त्रिज्याएँ r1,r2 तथा r3 है, (जहाँ r1<r2<r3 ) को दी हुई आकृति में दर्शाया गया है। r2, का मान क्या है?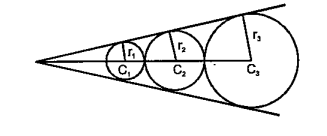
View SolutionProve that r1r2+r2r3+r3r1=14(a+b+c)2
View Solutionr1+r2−r3+r=4RsinC
View Solutionprovetˆ:△ABC,1r1+1r2+1r3=1r
View Solution