If the radius of the circum-circle of an isosceles triangle ABC is equal to AB(=AC), then angle A is
π6
π3
π2
2π3
The correct Answer is:D
To solve the problem, we need to find the angle A in an isosceles triangle ABC where the radius of the circumcircle (R) is equal to the lengths of the equal sides (AB = AC).
1. Identify the Given Information:
- Let AB = AC = R (the radius of the circumcircle).
- Let angle A be the angle opposite side BC.
2. Use the Sine Rule:
- According to the sine rule, we have:
asinA=bsinB=csinC=2R
- Here, a = BC, b = AC = R, and c = AB = R.
3. Set Up the Sine Rule for the Isosceles Triangle:
- Since AB = AC = R, we can write:
RsinB=2RandRsinC=2R
- This simplifies to:
sinB=12andsinC=12
4. Determine Angles B and C:
- The sine of an angle is 1/2 at 30 degrees:
B=30∘andC=30∘
5. Calculate Angle A:
- The sum of angles in a triangle is 180 degrees:
A+B+C=180∘
- Substituting the values of B and C:
A+30∘+30∘=180∘
- Simplifying gives:
A+60∘=180∘
- Therefore:
A=180∘−60∘=120∘
6. Convert Angle A to Radians:
- To express angle A in radians:
A=120×π180=2π3
Final Result:
Thus, angle A is 120∘ or 2π3 radians.
- Let AB = AC = R (the radius of the circumcircle).
- Let angle A be the angle opposite side BC.
- According to the sine rule, we have:
asinA=bsinB=csinC=2R
- Here, a = BC, b = AC = R, and c = AB = R.
- Since AB = AC = R, we can write:
RsinB=2RandRsinC=2R
- This simplifies to:
sinB=12andsinC=12
- The sine of an angle is 1/2 at 30 degrees:
B=30∘andC=30∘
- The sum of angles in a triangle is 180 degrees:
A+B+C=180∘
- Substituting the values of B and C:
A+30∘+30∘=180∘
- Simplifying gives:
A+60∘=180∘
- Therefore:
A=180∘−60∘=120∘
- To express angle A in radians:
A=120×π180=2π3
Thus, angle A is 120∘ or 2π3 radians.
Topper's Solved these Questions
- BOOK - ML KHANNACHAPTER - PROPERTIES OF TRIANGLES EXERCISE - Problem Set (4)(TRUE AND FALSE)9videos
PROPERTIES OF TRIANGLES
- BOOK - ML KHANNACHAPTER - PROPERTIES OF TRIANGLES EXERCISE - Problem Set (4)(FILL IN THE BLANKS)3videos
PROPERTIES OF TRIANGLES
- BOOK - ML KHANNACHAPTER - PROPERTIES OF TRIANGLES EXERCISE - Problem Set (3)(FILL IN THE BLANKS)2videos
PROPERTIES OF TRIANGLES
- BOOK - ML KHANNACHAPTER - PROGRESSIONS EXERCISE - MISCELLANEOUS EXERCISE (ASSERTION/REASON)1videos
PROGRESSIONS
- BOOK - ML KHANNACHAPTER - RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINEEXERCISE - COMPREHENSION11videos
RECTANGULAR CARTESIAN CO-ORDINATE SYSTEM AND THE STRAIGHT LINE
Similar Questions
Knowledge Check
- Question 1 - Select One
In an isosceles ΔABC, if AC=BC and AB2=2AC2 then ∠C=?
A30∘B45∘C60∘D90∘ - Question 2 - Select One
In an isosceles triangle ABC, AB=AC and ∠A=3∠B. Find ∠C.
A36∘B32∘C28∘D40∘ - Question 3 - Select One
In an isosceles triangle ABC, AB=AC and ∠A=3∠B. Find ∠C.
A36∘B32∘C28∘D40∘
O is the circumentre of the isosceles △ABC. Given that AB= AC = 17 cm and BC = 16 cm. The radius of the circle is
समद्विबाहु △ABC का परिकेन्द्र O हैं यह मानतें हुए कि AB=AC = 17 से.मी. और BC=16 से.मी., वृत्त की त्रिज्या बताए ?View SolutionIf ABC is an isosceles triangle with ∠C=90∘ and AC=5 cm, then AB is:
View SolutionIn the adjoining figure, P and Q are two points on equal sides AB and AC of a isosceles triangle ABC such that AP = AQ, then
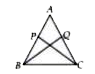 View Solution
View SolutionIn an isosceles triangle ABC,AB=AC,XY∣∣BC. If ∠A=30∘, then ∠BXY=?
View SolutionA statements of Assertion (A) is followed by a statement of Reason (R ). Mark the correct choice as.
Assertion (A): ABC is an isoseles triangle right triangle , right angled at C. Then AB2=3AC2.
Reason (R ): In an isosceles triangle ABC if AC = BC and AB2=2AC2 then ∠C=90∘.View Solution

