Seg Pm is a median of ΔPQR.PM=9andPQ2+PR2=290, then find QR.
Text Solution
The correct Answer is:QR=16
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - HOTS1videos
PYTHAGORS THEORM
- BOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - UNIQUE PRACTICE SESSION MCQ.S (3 MARKS QUESTION )6videos
PYTHAGORS THEORM
- BOOK - UNIQUE PUBLICATIONCHAPTER - PROBABILITY EXERCISE - PROBLEM SET 523videos
PROBABILITY
- BOOK - UNIQUE PUBLICATIONCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNMENT6videos
QUADRATIC EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In a triangle PQR, PQ=20 cm and PR =6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of the above - Question 2 - Select One
In a triangle PQR, PQ = 20 cm and PR = 6 cm, the side QR is :
Aequal to 14 cmBless than 14 cmCgreater than 14 cmDnone of these - Question 3 - Select One
In ΔDEFandΔPQR, if PQ =DE, EF=PR and FD =QR, then
AΔDEF≅ΔRPQBΔDEF≅ΔQPRCΔDEF≅ΔQRPDΔDEF≅ΔPQR
In ΔPQR ,seg PM is a median , PM=9 and PQ∘+PR2=290. Find the length of QR.
View SolutionSeg PM is a median of ΔPQR. If PQ=40,PR=42 and PM =29, find QR.
View SolutionIn ΔPQR, seg PM is median. PM=9, PQ2+PR2=290 then find length of seg QR.
View SolutionIn ΔPQR,∠PQR=90∘,
seg QS⊥ seg PR then find x,y,z.View Solution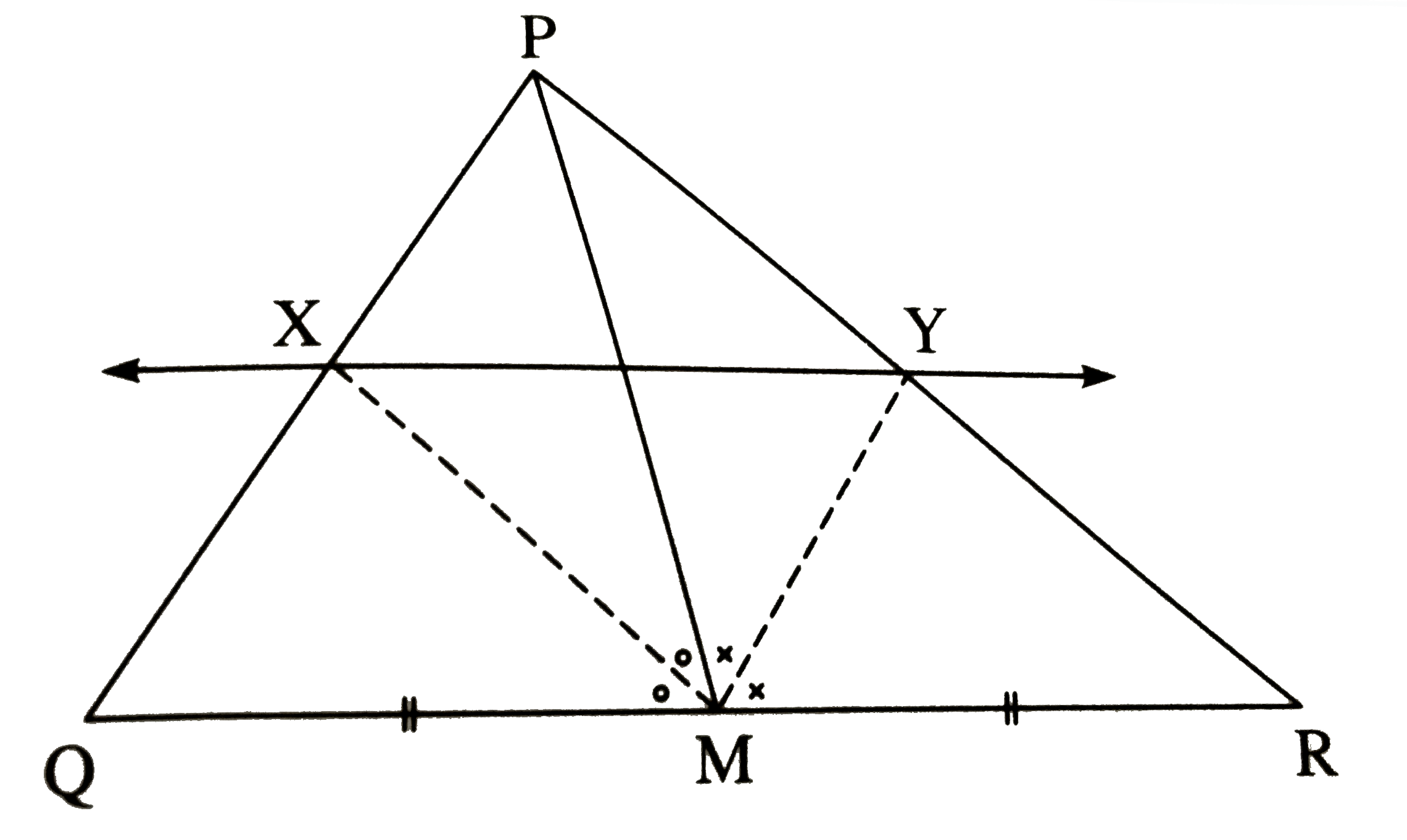
In ΔPQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR interesect side PQ and side PR in points X and Y respectively. Prove that XY∣∣QR.
Complete the proof byfilling in the boxes:View Solution


