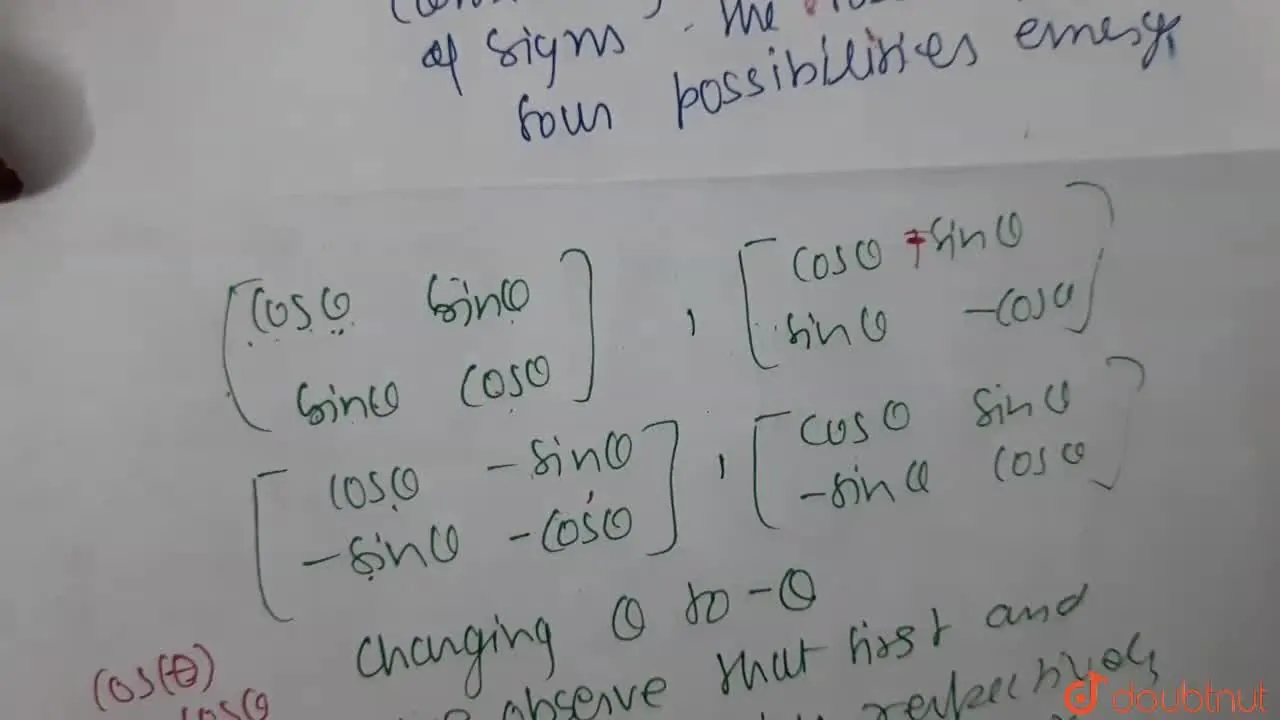Show that every real orthogonal matrix is of any one of the forms
Video Solution
Text Solution
Let be a 2-rowed real orthogonal matrix.
From
As , from the 1st and 3rd relations it follows that for i=1,2
then transforms to
according as we take same or different signs in the equations for and
Considering all combination of signs the following four possibilities emerge.
Changing to , we observe that first and 2nd matrices respectively coincides with 4th and 3rd matrices, so that we have only two types of 2-rowed real orthogonal matrices, viz
|
Updated on:21/07/2023
Related Playlists
- BOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Example 211videos
MATRICES
- BOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Example 221videos
MATRICES
- BOOK - AAKASH INSTITUTECHAPTER - MATRICESEXERCISE - Example 191videos
MATRICES
- BOOK - AAKASH INSTITUTECHAPTER - MATHEMATICAL REASONINGEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)15videos
MATHEMATICAL REASONING
- BOOK - AAKASH INSTITUTECHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section-J (Aakash Challengers Questions)7videos
PERMUTATIONS AND COMBINATIONS
Similar Questions
Evaluate : ∣∣∣cosθ−sinθsinθcosθ∣∣∣
View SolutionIf A = (cosθ−sinθsinθcosθ) then
View Solutioncosθ[cosθ−sinθsinθcosθ]+sinθ[sinθcosθ−cosθsinθ]=?
View SolutionEvaluate-
∣∣∣cosθsinθsinθcosθ∣∣∣View SolutionEvaluate the determinants in ∣∣∣cosθ−sinθsinθcosθ∣∣∣
View Solutionprove that- sinθ+1−cosθcosθ−1+sinθ=1+sinθcosθ
View SolutionifA=[cosθsinθ−sinθcosθ], then AAT=?
View SolutionLet A=[cosθ−sinθ−sinθ−cosθ] then inverse of A is
View SolutionShow that cosθ.[cosθsinθ−sinθcosθ]+sinθ.[sinθ−cosθcosθsinθ]=I.
View SolutionSimplify:
cosθ[cosθsinθ−sinθcosθ]+sinθ[sinθ−cosθcosθsinθ]View Solution