Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Video Solution
Text Solution
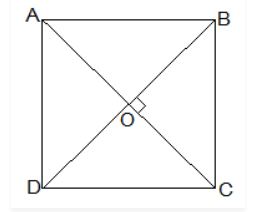
From ΔAOB and ΔCOD,
AO=CO (Diagonals bisect each other)
∠AOB=∠COD (Vertically opposite)
OB=OD (Diagonals bisect each other)
ΔAOB≅ΔCOD [SAS congruency]
Thus,
AB=CD [CPCT] — (i)
also,
∠OAB=∠OCD (Alternate interior angles)
⇒AB∣∣CD
Now,
In ΔAOD and ΔCOD,
AO=CO (Diagonals bisect each other)
∠AOD=∠COD (Vertically opposite)
OD=OD (Common)
ΔAOD≅ΔCOD [SAS congruency]
Thus,
AD=CD [CPCT] — (ii)
also,
AD=BC and AD=CD
⇒AD=BC=CD=AB — (ii)
also, ∠ADC=∠BCD [CPCT]
and ∠ADC+∠BCD=180∘ (co-interior angles)
⇒2∠ADC=180∘
⇒∠ADC=90∘ — (iii)
One of the interior angles is right angle.
Thus, from (i), (ii), and (iii) given quadrilateral ABCD is a square.
Hence Proved.
|
Topper's Solved these Questions
- QUADRILATERALSBOOK - NCERTCHAPTER - QUADRILATERALSEXERCISE - SOLVED EXAMPLES
8 Videos
- QUADRILATERALSBOOK - NCERTCHAPTER - QUADRILATERALSEXERCISE - SOLVED EXAMPLES
8 Videos
- PROBABILITYBOOK - NCERTCHAPTER - PROBABILITYEXERCISE - SOLVED EXAMPLES
10 Videos
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 14.1
2 Videos
Similar Questions
Knowledge Check
If the diagonals of a quadrilateral are equal and bisect each other at right angles, then the quadrilateral is a
AreactangleBsquareCrhombusDtrapezium
Show that the diagonals of a square are equal and bisect each other at right angles.
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View SolutionThe diagonals of a rectangle are equal and bisect each other
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
View SolutionIf the diagonals of a quadrilateral are equal and bisect each other, then the quadrilateral is a
View SolutionThe diagonals of a rhombus are unequal and bisect each other at right angle
View SolutionShow that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus
View Solution