Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
To prove that of all line segments drawn from a given point not on a line, the perpendicular line segment is the shortest, we can follow these steps:
Step 1: Define the Elements
Let P be a point not on line L. We will draw several line segments from point P to line L.
Step 2: Draw the Perpendicular Line Segment
Draw a perpendicular line segment from point P to line L. Let this perpendicular line segment be PM, where M is the foot of the perpendicular from P to L.
Step 3: Draw Other Line Segments
Now, draw another line segment PN from point P to some point N on line L such that N is not directly below P. This line segment PN will form an angle θ with the perpendicular line segment PM.
Step 4: Analyze the Triangles
Consider the triangle PMN. By the properties of triangles, we know that the length of the hypotenuse PN is always greater than the length of one of the other sides PM (the height). This is due to the triangle inequality theorem.
Step 5: Apply the Triangle Inequality
According to the triangle inequality theorem:
PN>PM
This means that any line segment drawn from point P to line L that is not perpendicular will be longer than the perpendicular segment PM.
Step 6: Conclusion
Since PM is the only line segment that is perpendicular to line L and all other segments PN are longer than PM, we can conclude that the perpendicular line segment is the shortest of all line segments drawn from point P to line L.
Final Statement
Thus, we have shown that of all line segments drawn from a given point not on a line, the perpendicular line segment is indeed the shortest.
---
Let P be a point not on line L. We will draw several line segments from point P to line L.
Draw a perpendicular line segment from point P to line L. Let this perpendicular line segment be PM, where M is the foot of the perpendicular from P to L.
Now, draw another line segment PN from point P to some point N on line L such that N is not directly below P. This line segment PN will form an angle θ with the perpendicular line segment PM.
Consider the triangle PMN. By the properties of triangles, we know that the length of the hypotenuse PN is always greater than the length of one of the other sides PM (the height). This is due to the triangle inequality theorem.
According to the triangle inequality theorem:
PN>PM
This means that any line segment drawn from point P to line L that is not perpendicular will be longer than the perpendicular segment PM.
Since PM is the only line segment that is perpendicular to line L and all other segments PN are longer than PM, we can conclude that the perpendicular line segment is the shortest of all line segments drawn from point P to line L.
Thus, we have shown that of all line segments drawn from a given point not on a line, the perpendicular line segment is indeed the shortest.
Similar Questions
Of all the line segments that can be drawn to a given line, from a point, not lying on it, the perpendicular line segment is the shortest. GIVEN : A straight line l and a point P not lying on l. PM⊥l and N is any point on 1 other than M. TO PROVE : PM<PN
View SolutionTo divide a line segment in a given ratio.
View Solution
Knowledge Check
- Question 1 - Select One
A line segment has _________ end points.
A0B1C2D4
A line segments has two end points.
View SolutionDraw a line segment EF equal to a given line segment AB
View SolutionIs line a part of line segments ?
View SolutionConstruct the perpendicular bisector of the line segment PQ.
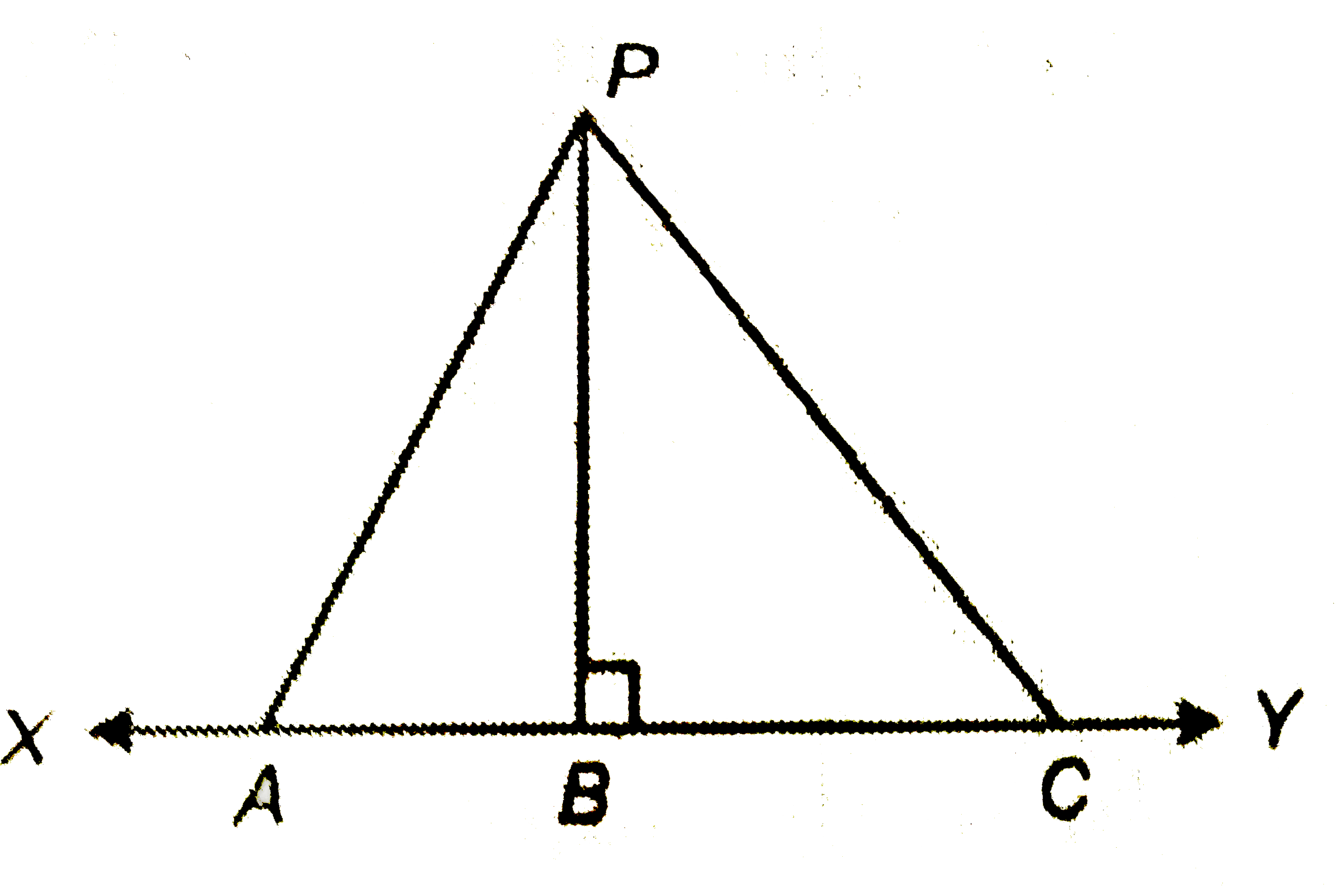
View SolutionIn the adjoining figure, line segment PA,PB and PC are drawn from point P to line XY. Here PB is perpendicular to XY.
(i) What is the nature of the angles formed by line segment PA and PC from XY ?
(ii) Which line segment is the smallest in the segment PA, PB and PC ?
 View Solution
View SolutionIf the extremities of a line segment of length l moves in two fixed perpendicular straight lines, then the locus of the point which divides this line segment in the ratio 1 : 2 is-
View SolutionDraw a line segment PQ of length 8.4cm. Draw the perpendicular bisector of this line segment.
View Solution

