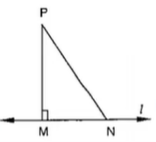
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
To show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest, we can follow these steps:
1. Identify the Points and Line:
Let point P be the given point not on the line L. We will draw a perpendicular line segment from point P to line L.
2. Draw the Perpendicular Segment:
Draw the perpendicular line segment from point P to line L. Let the foot of the perpendicular from P to line L be point O. Thus, OP is the perpendicular segment.
3. Consider Another Line Segment:
Now, consider any other line segment PM where M is any point on line L that is not the foot of the perpendicular (i.e., M≠O).
4. Form a Triangle:
The points P, O, and M form a triangle POM.
5. Analyze the Angles:
In triangle POM, we know that ∠POM is a right angle (90 degrees) because OP is perpendicular to L. Therefore, by the angle sum property of triangles, we have:
∠P+∠M+∠O=180∘
Since ∠O=90∘, we can write:
∠P+∠M=90∘
6. Use Properties of Angles:
Since ∠P+∠M=90∘, both ∠P and ∠M must be less than 90 degrees. This means that ∠P<90∘ and ∠M<90∘.
7. Apply the Side-Angle Relationship:
According to the properties of triangles, the side opposite to a larger angle is longer. Thus, since ∠O (90 degrees) is greater than both ∠P and ∠M, the side opposite ∠O (which is PM) must be longer than the sides opposite ∠P and ∠M (which is OP).
8. Conclude the Result:
Therefore, we can conclude that:
OP<PM
This shows that the perpendicular line segment OP is shorter than any other line segment PM drawn from point P to line L.
Conclusion:
Thus, we have shown that of all line segments drawn from a given point not on it, the perpendicular line segment is indeed the shortest.
Let point P be the given point not on the line L. We will draw a perpendicular line segment from point P to line L.
Draw the perpendicular line segment from point P to line L. Let the foot of the perpendicular from P to line L be point O. Thus, OP is the perpendicular segment.
Now, consider any other line segment PM where M is any point on line L that is not the foot of the perpendicular (i.e., M≠O).
The points P, O, and M form a triangle POM.
In triangle POM, we know that ∠POM is a right angle (90 degrees) because OP is perpendicular to L. Therefore, by the angle sum property of triangles, we have:
∠P+∠M+∠O=180∘
Since ∠O=90∘, we can write:
∠P+∠M=90∘
Since ∠P+∠M=90∘, both ∠P and ∠M must be less than 90 degrees. This means that ∠P<90∘ and ∠M<90∘.
According to the properties of triangles, the side opposite to a larger angle is longer. Thus, since ∠O (90 degrees) is greater than both ∠P and ∠M, the side opposite ∠O (which is PM) must be longer than the sides opposite ∠P and ∠M (which is OP).
Therefore, we can conclude that:
OP<PM
This shows that the perpendicular line segment OP is shorter than any other line segment PM drawn from point P to line L.
Thus, we have shown that of all line segments drawn from a given point not on it, the perpendicular line segment is indeed the shortest.
Similar Questions
Knowledge Check
A line segment.___
AHas only one end pointBHas two end pointsCHas length and widthDExtend endlessly in both directions
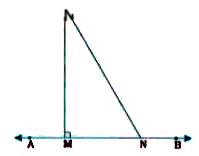
Of all the line segments that can be drawn to a given line, from a point, not lying on it, the perpendicular line segment is the shortest. GIVEN : A straight line l and a point P not lying on l. PM⊥l and N is any point on 1 other than M. TO PROVE : PM<PN
View Solution: To divide a line segment in a given ratio.
View SolutionShow that the locus of a point, equidistant from the endpoints of a line segment, is the perpendicular bisector of the segment
View SolutionTo construct the perpendicular bisector of a given line segment.
View SolutionOf all the line segments drawn from a point P to a line m not containing P, let PD be the shortest. If B and C are points on m such that D is the mid-point of BC , prove that PB=PC.
View SolutionOf all the lines segments drawn from a point P to a line m not containing P, let PD be the shortest. If B and C are points on m such that D is the mid-point of BC , prove that PB=PC
View SolutionTwo line segments may intersect at two points
View Solution