Show that (p∧q)∨(~p)∨(p∧~q) is a tautology Solution in Tamil
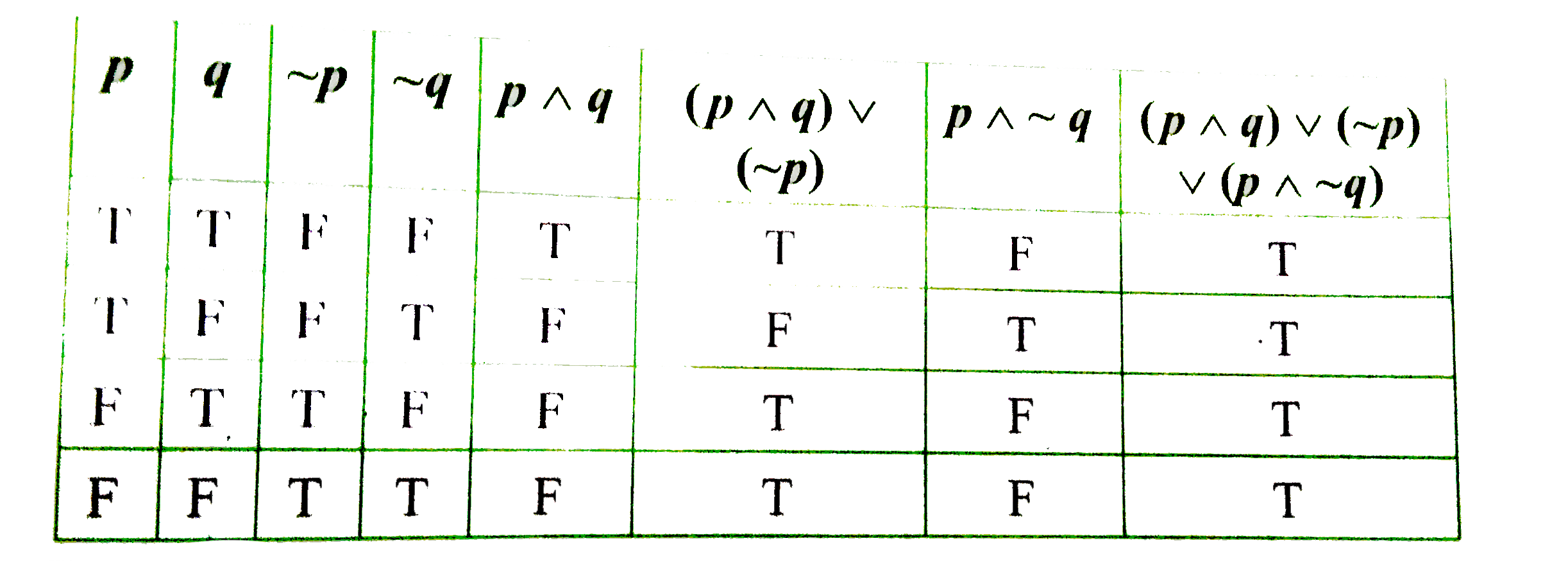
fol all possible truth values of p and q, the compound statement
(p∧q)∨(~p)∨(p∧~q) is true.
Thus, (p∧q)∨(~p)∨(p∧~q) is a tautology .
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise (Single)38videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - JEE Previous Year10videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise 10.18videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE Previous Year5videos
LOGARITHM AND ITS PROPERTIES
- BOOK - CENGAGECHAPTER - MATRICESEXERCISE - Multiple Correct Answer7videos
MATRICES
Similar Questions
Which of the following is not a statement.
02:30View SolutionStatement-1: ~(p↔~q) is equivalent to (p↔q).
Statement-2: ~(p↔~q) is a tautology.04:23View SolutionWrite down the truth table for the compound statements :
(~p∨q)∧(~p∧~q)02:37View SolutionShow that the equation esinx−e−sinx−4=0 has no real solution.
02:20View SolutionIf A=⎡⎢⎣100101010⎤⎥⎦, then
02:36View SolutionThe statement which is not a tautology is (p↔q)[(p→q)∧(q→q)] b. (p→q)∨(~p→q) c. (p∧q)−−−→p∨q d. (p∧q)∨[(p∨q)→˜q]
01:48View Solutionlet (i) (p∨q)∧(p∨~q),(ii)(p∧q)∧(q∨~q),(iii).(p∨q)∧(p∨~q),(iv)(p∨q)∨(p∧~q) then which one is tautology
01:53View SolutionShow that (p∧q)∨(~p)∨(p∧~q) is a tautology
02:26View SolutionSimplify (p∨q)∧(p∨~q).
03:55View SolutionShow that (p∧¬q)∨(¬p∨q) is a tautology.
05:07View SolutionShow that (p∧q)→(p∨q) is a tautology.
05:16View SolutionShow that [¬p∨¬q]∨p is a tautology.
03:51View SolutionObserve the following statements
I : The dual of [~p∧q)]∨[p∧{~(q∨~s)}] is [~(p∨q)]∧[p∨{~(q∧~s)}]
II : The dual of ~p∧[(~q)∧(p∨q)∧~r] is ~p∨[~q)∨(p∧q)∨~r]
The true statements in the above is/are :View SolutionShow that (p∧q)∨(~p)∨(p∧~q) is a tautology
05:05View SolutionConstruct truth tables for the following and indicate which of these are tautologies (p∨≈q)∧(q∨≈p)
03:59View Solution
