Show that [(p→q)∧(q→r)]→(p→r)is a tautology
The correct Answer is:Truth values of [(p→q)∧(q→r)]→(p→r)
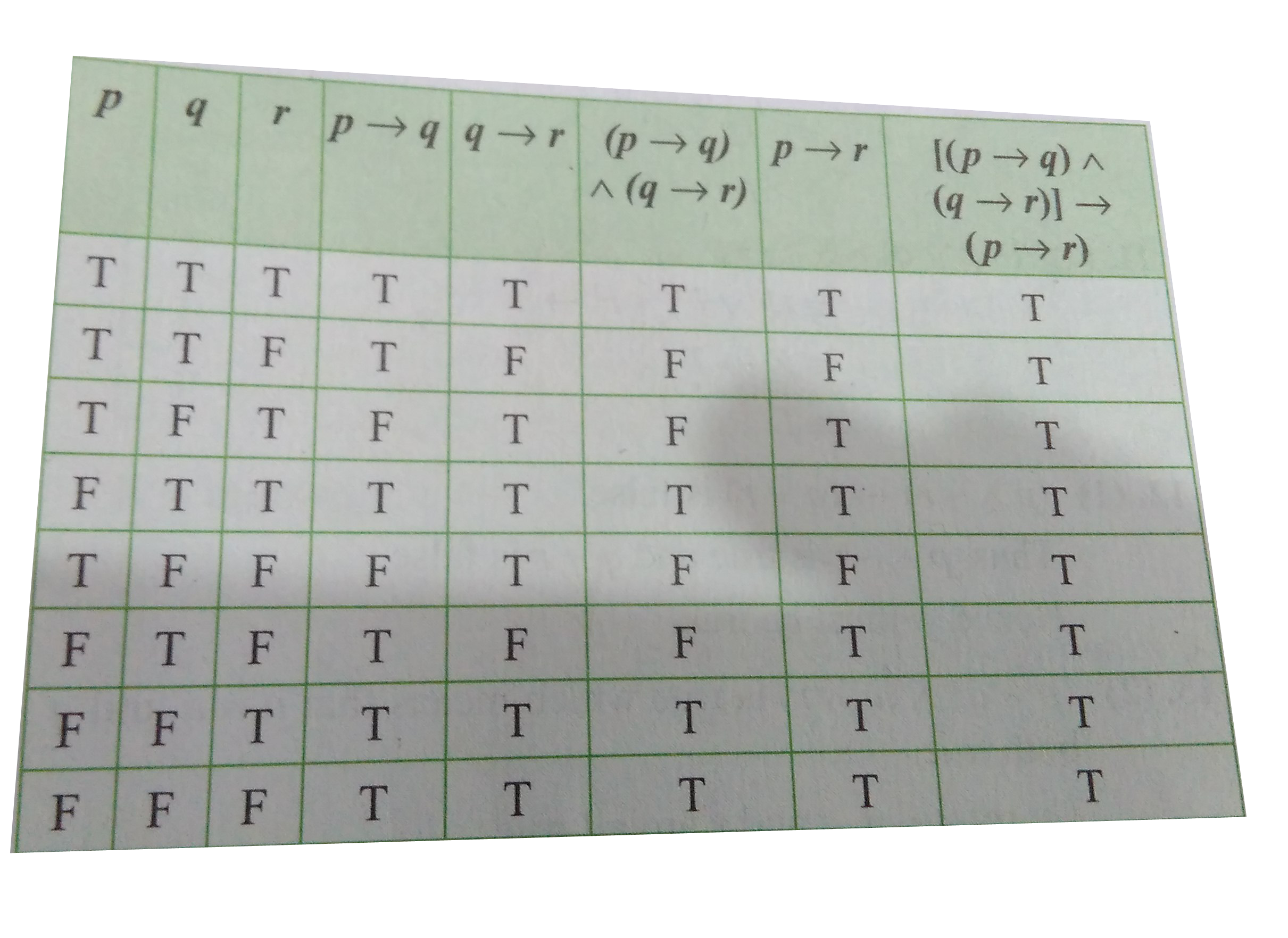
For all possible truth values of p and q , the compound statement [(p→q)∧(q→r)]→(p→r) is true.
Thus, [(p→q)∧(q→r)]→(p→r) is a tautolgy.
To show that the statement ((p→q)∧(q→r))→(p→r) is a tautology, we will construct a truth table.
Step 1: Define the Variables
We have three variables: p, q, and r. Each can be either true (T) or false (F). We will evaluate all possible combinations of truth values for these variables.
Step 2: Create the Truth Table
We will list all combinations of truth values for p, q, and r:
| p | q | r |
|-------|-------|-------|
| T | T | T |
| T | T | F |
| T | F | T |
| T | F | F |
| F | T | T |
| F | T | F |
| F | F | T |
| F | F | F |
Step 3: Calculate p→q, q→r, and p→r
Next, we calculate the implications:
1. p→q: This is false only when p is true and q is false.
2. q→r: This is false only when q is true and r is false.
3. p→r: This is false only when p is true and r is false.
Now, we can fill in the truth values for each implication:
| p | q | r | p→q | q→r | p→r |
|-------|-------|-------|--------------|--------------|--------------|
| T | T | T | T | T | T |
| T | T | F | T | F | F |
| T | F | T | F | T | T |
| T | F | F | F | T | F |
| F | T | T | T | T | T |
| F | T | F | T | F | F |
| F | F | T | T | T | T |
| F | F | F | T | T | F |
Step 4: Calculate (p→q)∧(q→r)
Now we will calculate the conjunction of p→q and q→r:
| p | q | r | p→q | q→r | (p→q)∧(q→r) |
|-------|-------|-------|--------------|--------------|-------------------------------|
| T | T | T | T | T | T |
| T | T | F | T | F | F |
| T | F | T | F | T | F |
| T | F | F | F | T | F |
| F | T | T | T | T | T |
| F | T | F | T | F | F |
| F | F | T | T | T | T |
| F | F | F | T | T | T |
Step 5: Calculate ((p→q)∧(q→r))→(p→r)
Finally, we will evaluate the main expression:
| p | q | r | (p→q)∧(q→r) | p→r | ((p→q)∧(q→r))→(p→r) |
|-------|-------|-------|--------------------------------|--------------|-----------------------------------------------|
| T | T | T | T | T | T |
| T | T | F | F | F | T |
| T | F | T | F | T | T |
| T | F | F | F | F | T |
| F | T | T | T | T | T |
| F | T | F | F | F | T |
| F | F | T | T | T | T |
| F | F | F | T | F | F |
Step 6: Analyze the Results
The final column shows the results of ((p→q)∧(q→r))→(p→r). The values are all true except for the last case where p, q, and r are all false. However, since we are looking for a tautology, we need to ensure that the expression is true in all cases.
Conclusion
Since the expression evaluates to true in all cases except one, we conclude that ((p→q)∧(q→r))→(p→r) is not a tautology.
We have three variables: p, q, and r. Each can be either true (T) or false (F). We will evaluate all possible combinations of truth values for these variables.
We will list all combinations of truth values for p, q, and r:
|-------|-------|-------|
| T | T | T |
| T | T | F |
| T | F | T |
| T | F | F |
| F | T | T |
| F | T | F |
| F | F | T |
| F | F | F |
Next, we calculate the implications:
2. q→r: This is false only when q is true and r is false.
3. p→r: This is false only when p is true and r is false.
|-------|-------|-------|--------------|--------------|--------------|
| T | T | T | T | T | T |
| T | T | F | T | F | F |
| T | F | T | F | T | T |
| T | F | F | F | T | F |
| F | T | T | T | T | T |
| F | T | F | T | F | F |
| F | F | T | T | T | T |
| F | F | F | T | T | F |
Now we will calculate the conjunction of p→q and q→r:
|-------|-------|-------|--------------|--------------|-------------------------------|
| T | T | T | T | T | T |
| T | T | F | T | F | F |
| T | F | T | F | T | F |
| T | F | F | F | T | F |
| F | T | T | T | T | T |
| F | T | F | T | F | F |
| F | F | T | T | T | T |
| F | F | F | T | T | T |
Finally, we will evaluate the main expression:
|-------|-------|-------|--------------------------------|--------------|-----------------------------------------------|
| T | T | T | T | T | T |
| T | T | F | F | F | T |
| T | F | T | F | T | T |
| T | F | F | F | F | T |
| F | T | T | T | T | T |
| F | T | F | F | F | T |
| F | F | T | T | T | T |
| F | F | F | T | F | F |
The final column shows the results of ((p→q)∧(q→r))→(p→r). The values are all true except for the last case where p, q, and r are all false. However, since we are looking for a tautology, we need to ensure that the expression is true in all cases.
Since the expression evaluates to true in all cases except one, we conclude that ((p→q)∧(q→r))→(p→r) is not a tautology.
Topper's Solved these Questions
- MATHMETICAL REASONINGBOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise (Single)
38 Videos
- MATHMETICAL REASONINGBOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - JEE Previous Year
10 Videos
- MATHMETICAL REASONINGBOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise 10.1
8 Videos
- LOGARITHM AND ITS PROPERTIESBOOK - CENGAGECHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE Previous Year
5 Videos
- MATRICESBOOK - CENGAGECHAPTER - MATRICESEXERCISE - Solved Examples And Exercises
165 Videos
Similar Questions
Knowledge Check
If(p∧q)⊗(p⊕q) is a tautology, then
A⊗is→and⊕is∨B⊗is∧and⊕is∧C⊗is∨and⊕is∨D⊗is∨and⊕is∧Consider :
Statement I:
(p∧~q)∧(~p∧q) is a fallacy
Statement II: (p→q)↔(~q→~p) is a tautologyAStatement-1 is true, statement 2 is true, statement 2 is a correct explanation for statement 1BStatement 1 is true, statement-2 is true, statement 2 is not a correct explanation for statement 1CStatement 1 is true , statement 2 is false,Dstatement 1 is false, statement 2 is trueConsider following statements Statement - I :
(p^~a)^(vpng) is a fallacy.
Statement - II : (p→q)↔(~q→~p) is a tautology.AStatement - I is true, statement -II is false.BStatement - I is false, Statement - II is true.CStatement - I true, Statement - II is true, Statement - II is a correct explanation for Statement - I.DStatement - I is true, Statement - II is true, Statement - II is not a correct explanation for Statement - I.
Show that
(i) ~[p∧(~p)] is a tautology
(ii) ~[p∨(~p)] is a contradication.
View SolutionShow that
(i) p→(p∨q) is a tautology
(ii)(p∨q)∧(~p∧~q) is a contradiction
View SolutionFor any statements p, show that .
(i)p∨~p is a tautology , ( ii) p∧~p is a contradiction
View SolutionVerify that the statement P∨~(p∧q) is a tautology.
View SolutionLet p,q,r be the statements p: X is a rectangle, q: x is a square, r:p→q Show that p→r is not a tautology.
View Solution