Show that (p∨q)→r≡(p→r)∧(q→r)
Video Solution
Text Solution
Truth table for (p∨q)→r and (p→r)∧(q→r).

It is evident from the last two columns that
(p∨q)→r≡(p→r)∧(q→r)
Note:
1p→q≡(~p)∨q
2.p↔q≡(p→q)∧(q→p)
3.p↔q≡(~p∨q)∧(p∨~q)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise 10.18videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise 10.25videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE Previous Year5videos
LOGARITHM AND ITS PROPERTIES
- BOOK - CENGAGECHAPTER - MATRICESEXERCISE - Solved Examples And Exercises165videos
MATRICES
Similar Questions
Knowledge Check
- Question 1 - Select One
p∧(q∧r)=(p∧q)∧r is
Adistributive lawBassociative lawCcommutative lawDNone of these - Question 2 - Select One
p∧(q∨r)≡(p∧q)∨(p∧r) is :
AAssociative lawBDistributiveCIdentity lawDAbsorption - Question 3 - Select One
The contrapositive of (p∨q)→r is
Ar→(p∨q)B~r→(p∨q)C~r→(~p∧~q)Dp→(q∨r)
Construct the truth table for the followings statements :
(a) (p∧q)→~p (b)(p∧q)→(p∨q)
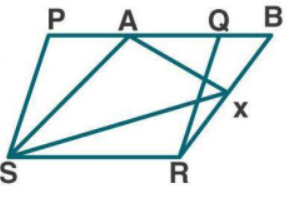
(c) (p∧q)→r (d)[p∧(~r)]→(q∨r)View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
 View Solution
View SolutionThree numbers p, q, r are such that pq=qr, where p,q,r>1 then the correct relation between q and r is :
View SolutionGiven 'p' and 'q' as true and 'r' as false, the truth values of ~p∧(q∨~r) and (p→q)∧r are respectively
View SolutionIf p, q, and r are the statements and (p∧q)∧(q∧r) is true, then
View Solution

