Show that [(p∨q)∨r]↔[p∨(q∨r)] is a tautology Solution in Bengali
Truth table of [(p∨q)∨r]↔[p∨(q∨r)]
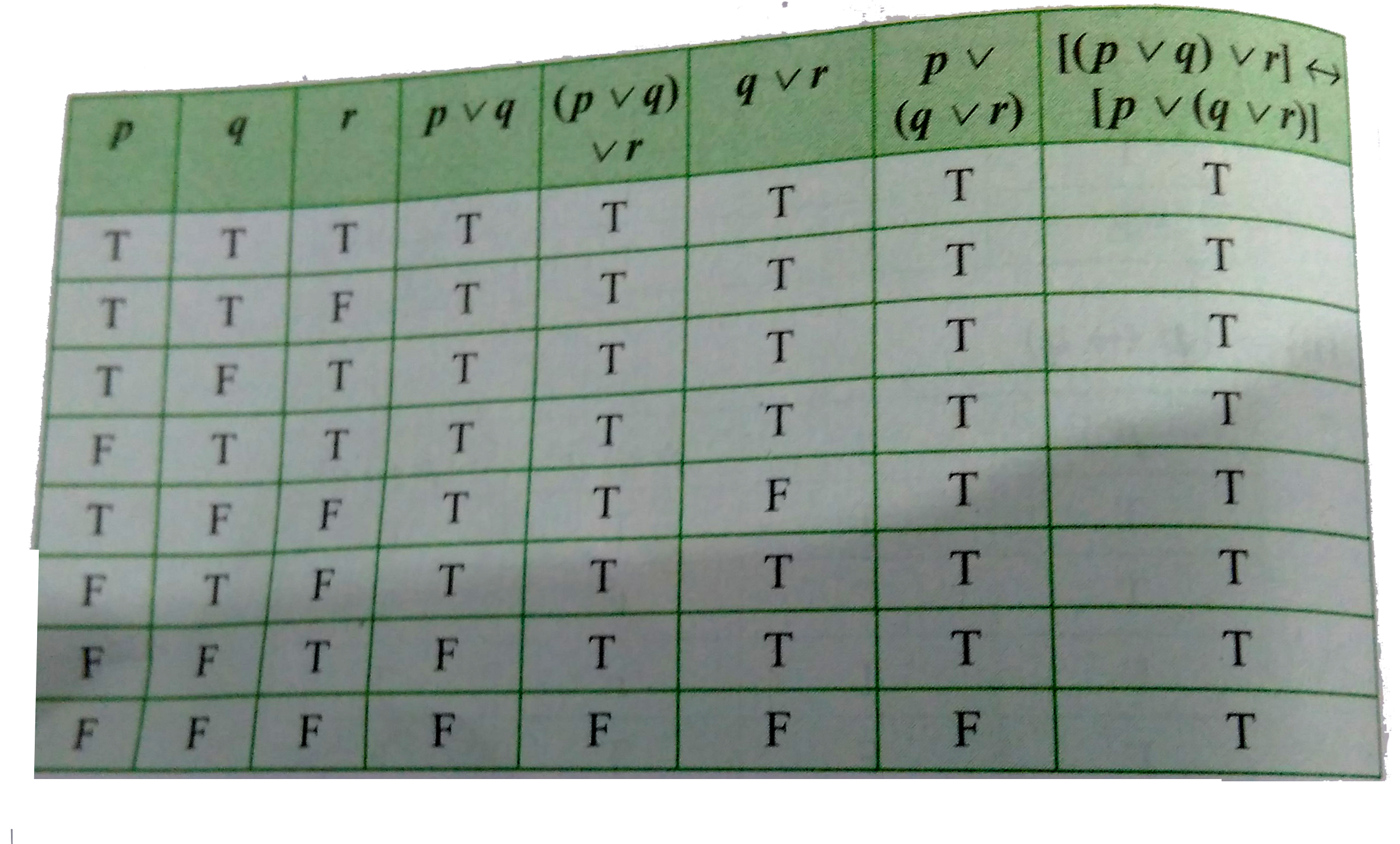
Thus, for all possible truth values of p,q and r , the compound statements : [p∨q)∨r]↔[p∨(q∨r)] is true.
∴[(p∨q)∨r]↔[p∨(q∨r)] is a tautology.
Topper's Solved these Questions
- MATHMETICAL REASONINGBOOK - CENGAGE PUBLICATIONCHAPTER - MATHMETICAL REASONINGEXERCISE - concept application
13 Videos
- MATHMETICAL REASONINGBOOK - CENGAGE PUBLICATIONCHAPTER - MATHMETICAL REASONINGEXERCISE - Single correct answer type
38 Videos
- LOGARITHM AND ITS PROPERTIESBOOK - CENGAGE PUBLICATIONCHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE ADVANCED
1 Videos
- MATRICESBOOK - CENGAGE PUBLICATIONCHAPTER - MATRICESEXERCISE - All Questions
509 Videos
Similar Questions
Write down the truth table for the compound statements :
(~p∨q)∧(~p∧~q)
View SolutionWhich of the following is not a statement.
View SolutionLet (x0,y0) be the solution of the following equations: (2x)1n2=(3y)1n3 31nx=21ny The x0 is 16 (b) 13 (c) 12 (d) 6
View SolutionIn which of the following type of matrix inverse does not exist always? a. idempotent b. orthogonal c. involuntary d. none of these
View SolutionFind the truth values of the following compound statements :
(i) P∧(q∧r) (ii)(p∨q)∨r
(iii) p∧(q∨r) (iv)(p∧q)∨r
View SolutionShow that
(i) p→(p∨q) is a tautology
(ii)(p∨q)∧(~p∧~q) is a contradiction
View SolutionShow that [(p∨q)∨r]↔[p∨(q∨r)] is a tautology
View Solutionसत्यमान सरणी से निम्न को सिद्ध कीजिये
p∨(q∨r)≡(p∨q)∨r
View Solutionयदि p,q,r कोई तीन कथन है तब सिद्ध कीजिये कि
(p∨q)∨r≡p∨(q∨r)
View SolutionThe dual of the statement p∨(q∨r)≡(p∨q)∨r is
View SolutionFind the truth values of the following compound statements :
(i) P∧(q∧r) (ii)(p∨q)∨r
(iii) p∧(q∨r) (iv)(p∧q)∨r
View SolutionShow that
(i) p→(p∨q) is a tautology
(ii)(p∨q)∧(~p∧~q) is a contradiction
View SolutionShow that [(p∨q)∨r]↔[p∨(q∨r)] is a tautology
View SolutionFind the truth values of the following compound statements :
(i) P∧(q∧r) (ii)(p∨q)∨r
(iii) p∧(q∨r) (iv)(p∧q)∨r
View SolutionShow that
(i) p→(p∨q) is a tautology
(ii)(p∨q)∧(~p∧~q) is a contradiction
View Solution
