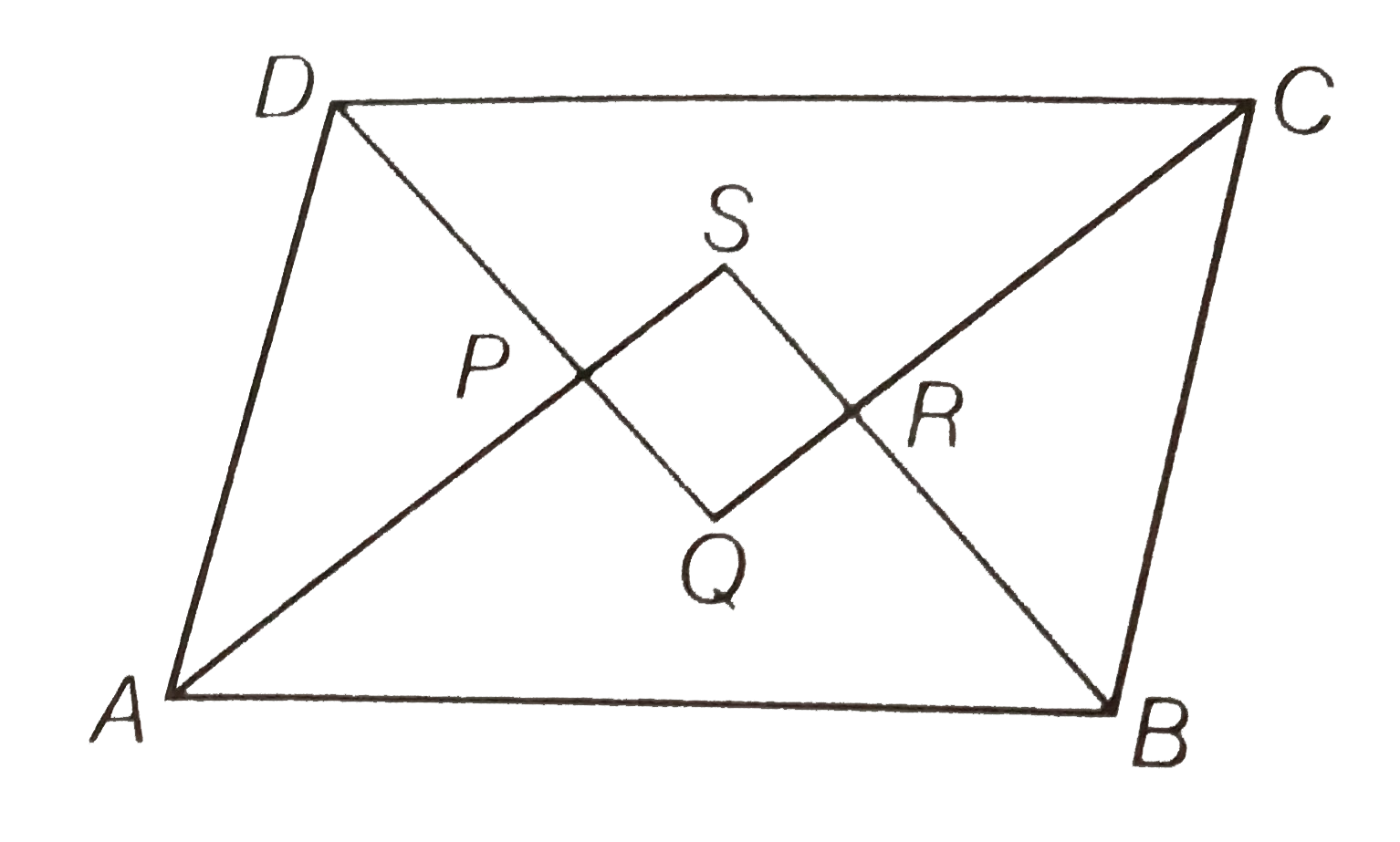
Show that the bisectors of angles of a parallelogram form a rectangle.

Video Solution

Text Solution

Verified by Experts

Let a parallelogram ABCD
As we know that $∠ P A S = ∠ R A B = \frac{1}{2} ∠ P A B$ 1
Similarly, $∠ C B Q = ∠ Q B A = \frac{1}{2} ∠ C B A$ _2
So, AD||BC then $∠ O A B + ∠ C A B = 180^{\circ}$
$\frac{1}{2} ∠ D A B + \frac{1}{2} ∠ C A B = 90^{\circ}$
$∠ R A B + ∠ R B A = 180^{\circ}$
Now, In $△ R A B$
$∠ R A B + ∠ A R B = 180^{\circ}$
$90^{\cdot} + ∠ A R B = 180^{\circ}$
$∠ A R B = 90^{\circ}$
Similarly, $∠ D P C = 90^{\circ}$
So, opposite angles are $90^{\circ}$
Hence, it is a rectangle.
$∴$ $∠ D A S = ∠ R A B = \frac{1}{2} ∠ D A B$ .

Updated on:21/07/2023