Show that the lines 4x+y−9=0,x−2y+3=0,5x−y−6=0 make equal intercepts on any line of slope 2.
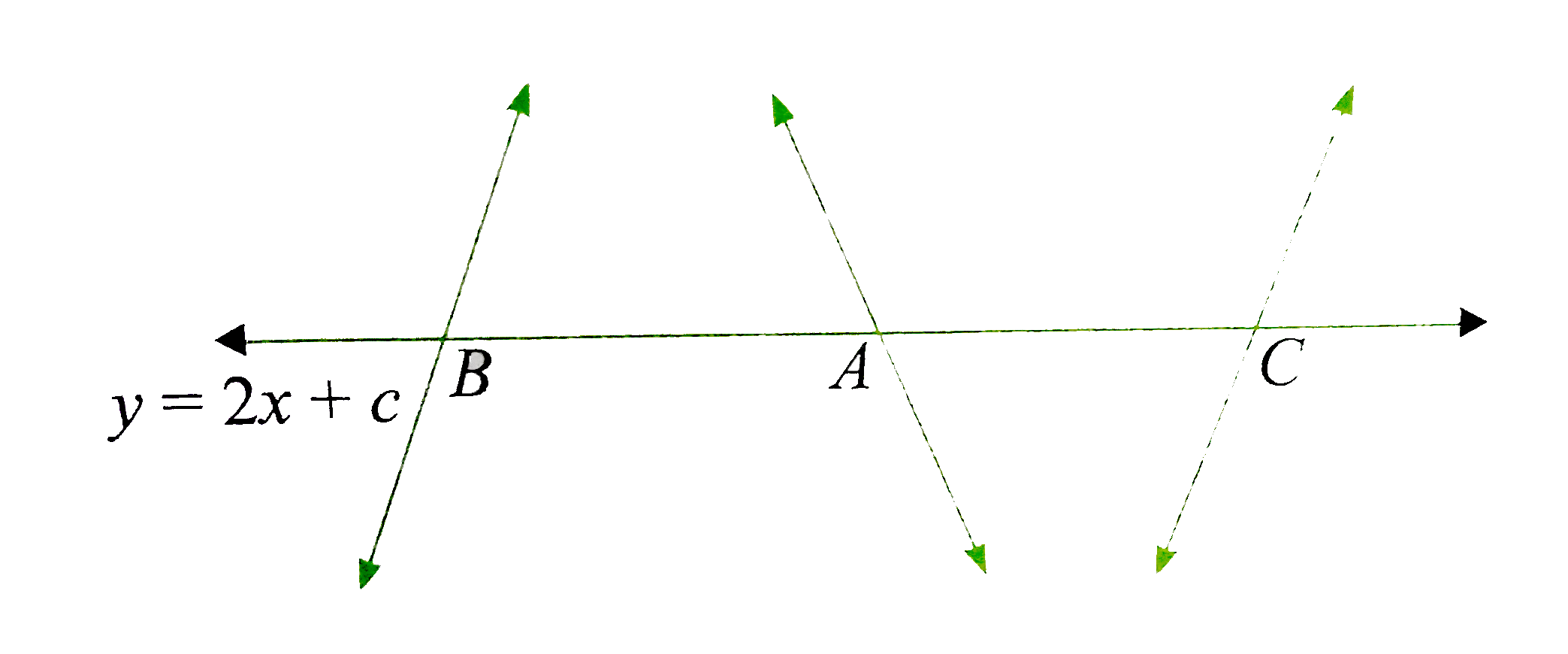
The given lines are
4x+y−9=0 (1)
x−2y+3=0 (2)
5x−y−6=0 (3)
Now, the equation of any line having slope (gradient) 2 will be
y=2x+c (4)
Let line (4) cuts line (1), (2), and (3) at A,B, and C. respectively.
Solving (1) and (4), we get
A≡(32−c6,3+2c3)
Similary,B≡(1−2cc,2−c3)
and C≡(2+c3,4+5c3)
Clearly , A is the middle point of BC, Hene, AB=AC.
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Knowledge Check
The lines x+2y−5=0,2x−3y+4=0,6x+4y−13=0
Aare concurrentBform a right angled triangleCform an isosceles triangleDform an equilateral triangle.Let the lines 4x−3y+10=0 and 4x−3y−30=0 make equal intercepts of 6 units with a circle (C ) whose centre lies on 2x+y=0, then the equation of the circle C is
Ax2+y2−2x+4y−20=0Bx2+y2−4x+8y−20=0Cx2+y2+2x−4y−20=0Dx2+y2−4x+8y−5=0A line passes through the point of intersection of the lines 3x+y+1=0 and 2x-y+3=0 and makes equal intercepts with axes. Then, equation of the line is
A5x+5y-3=0Bx+5y-3=0C5x-y-3=0D5x+5y+3=0
Find the equation of the line passing through the point of intersection of the lines 4x+7y−3=0and2x−3y+1=0, which has equal intercepts on the axes.
View SolutionFind the equation of the line passing through the intersection of the lines 4x+7y−3=0and2x−3y+1=0 that has equal intercepts on the axes.
View SolutionFind the equation of the line passing through the point of intersection of the lines 4x+7y−3=0and 2x−3y+1=0that has equal intercepts on the axes.
View SolutionA line passes through the point of intersection of the line 3x+y+1=0 and 2x−y+3=0 and makes equal intercepts with axes. Then, equation of the line is
View SolutionA line passes through the point of intersection of the lines 3x+y+1=0 and 2x-y+3=0 and makes equal intercepts with axis. Then, equation of the line is
View Solution
