Show that the locus of a point, equidistant from two intersecting lines in the plane, is a pair of lines bisecting the angles formed by the given lines.
Video Solution
Text Solution
Step I : We initially prove that any point equidistant from two given intersecting lines lies on one of of the lies bisecting the angles fromed by the given lines.
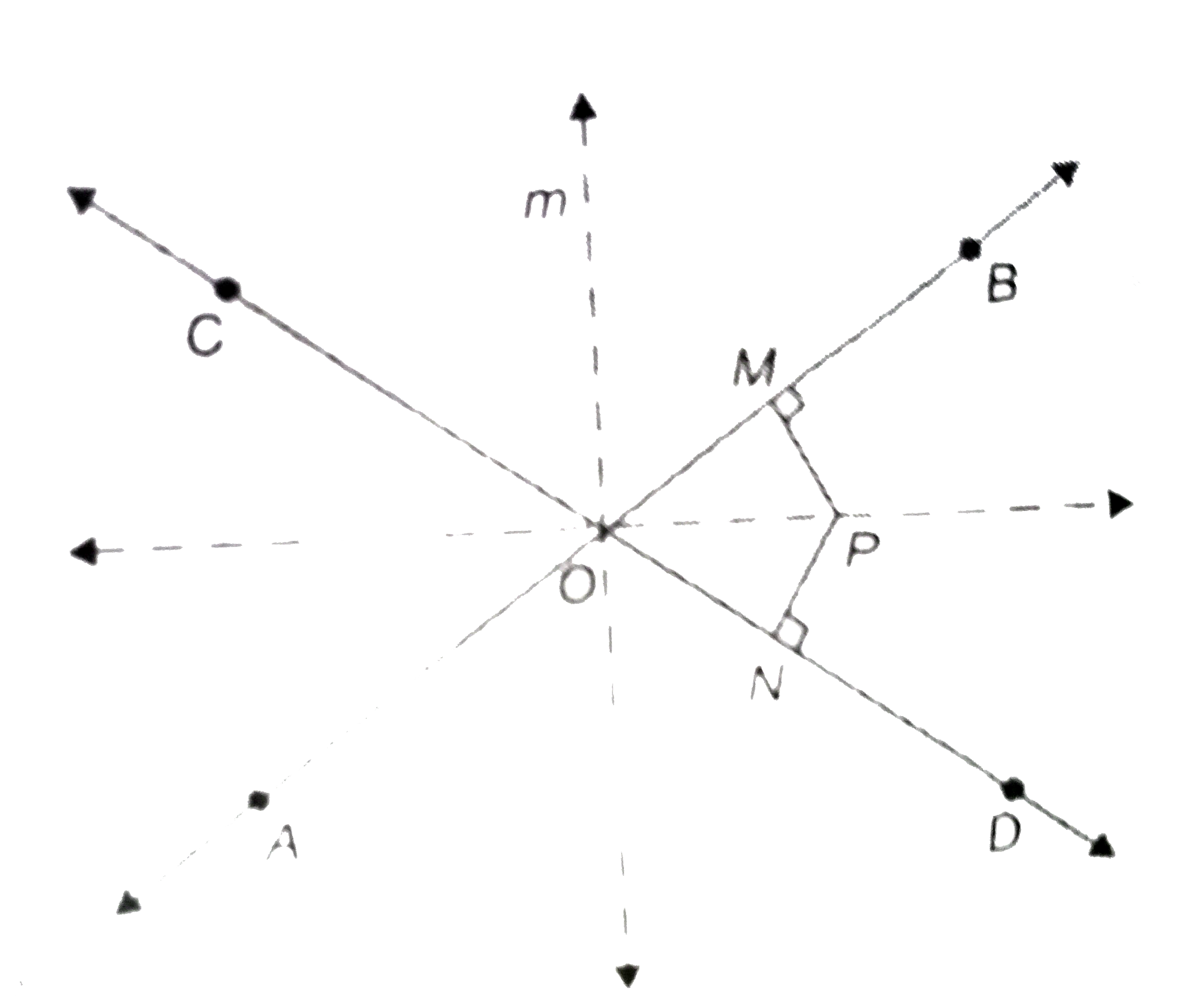
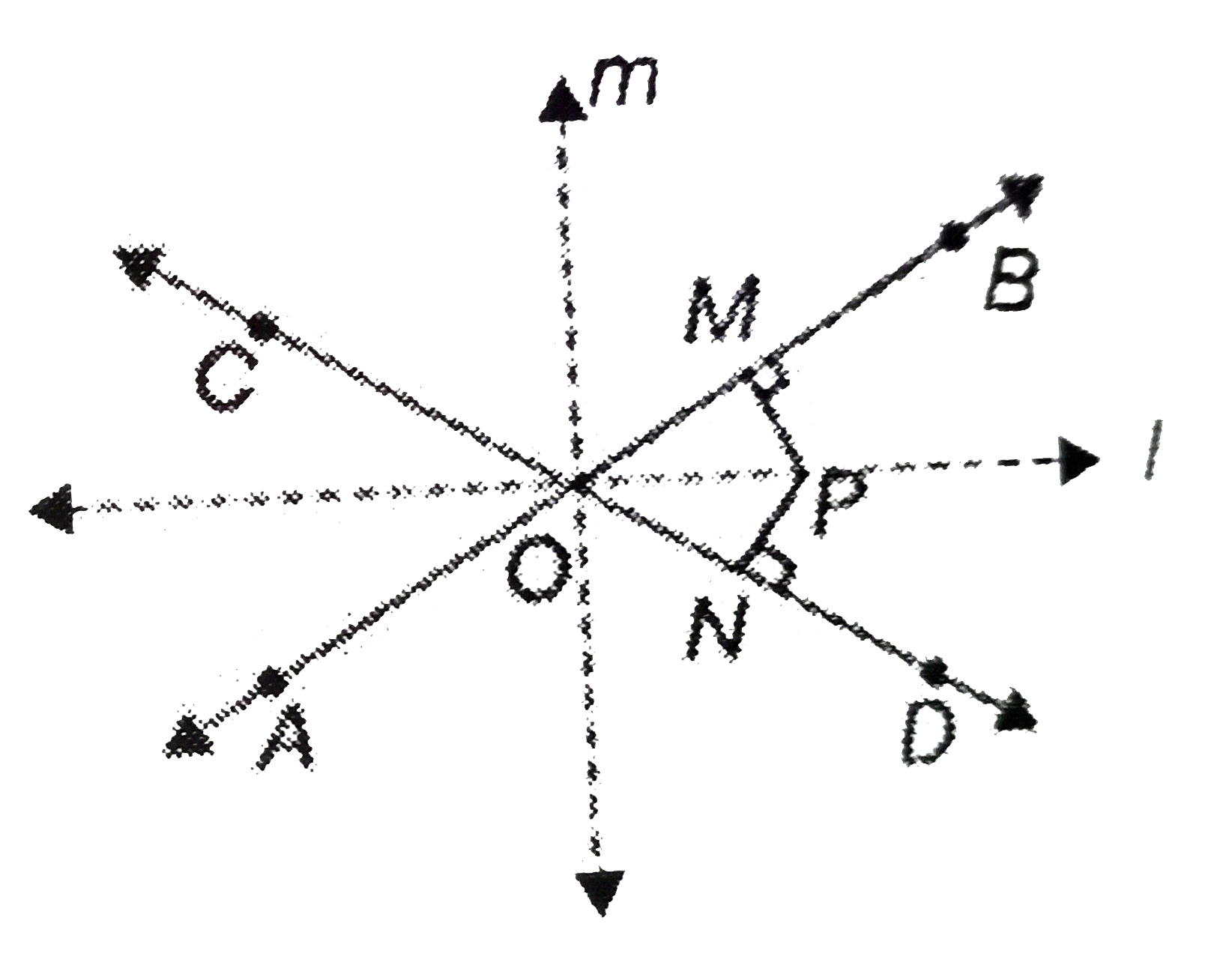
Given : ¯¯¯¯¯¯AB and ¯¯¯¯¯¯CD are two line intersecting a O. P is the point on the plane such that PM = PN
Line I is the bisector of ∠BOC and ∠AOC
LIne m is the bisector of ∠BOC and ∠AOD
To proves : P lies either on the line I or on the line m
Proof : In ΔPOM and ΔPON, PM = PN
OP is ommon side and ∠PMO=∠PNO=90∘
∴ By RHS congrunce property, ΔPOM≅ΔPON
So, ∠POM=∠PON, i.e P lies on the angles bisector of ∠BOD
As l is the bisector of ∠BOD and ∠AOC, P lies on the line l.
Similarly, if P lies in any of the regions of ∠BOC∠AOC or ∠AOD, such that it is equidistant from ¯¯¯¯¯¯AB and ¯¯¯¯¯¯CD then we can conclude that P lies on the angle bisector l or on the angle bisector m.
Step 2 : Now, we prove that any two point on the bisector of one of the angle formed by two intersecting lines is equidistant from the lines.
Given ¯¯¯¯¯¯AB and ¯¯¯¯¯¯CD, intersect at O lines l and m are the angle bisectors.
proof : Let l be the angle bisector of ∠BOD and ∠AOC and m be the angle bisector of ∠BOC and ∠AOD
Let P be a point on the angle bisector l, as shown in
If P coinclides with O, then P is equidistant line ¯¯¯¯¯¯AB and ¯¯¯¯¯¯CD
Suppose P is different O
Draw the perpendicular ¯¯¯¯¯¯¯PM and ¯¯¯¯¯¯PN from the point P onto the lines ¯¯¯¯¯¯AB and ¯¯¯¯¯¯CD respectively.
Then in ΔPOM=∠PON,∠PNO=∠PMO=90∘ and OP is a common side.
∴ By the AAS congruance property.
ΔPOM≅ΔPON
So, PN = PM ( ∵ The corresponding sides in congruent triangles.
That is P is equidistant from lies ¯¯¯¯¯¯AB and ¯¯¯¯¯¯CD
Hence, from Step I and Step II of the proof, it can be said that the locus of the point, which is equidistant from the two intersecting lines is the pari of the angle bisectors of the two pairs of vertically oppoiste angles formed by the lines.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOCUSEXERCISE - Very short Answer Question15videos
LOCUS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOCUSEXERCISE - Short Answer Question8videos
LOCUS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS AND INEQUATIONSEXERCISE - level 310videos
LINEAR EQUATIONS AND INEQUATIONS
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LOGARITHMSEXERCISE - Level 3 MCQ15videos
LOGARITHMS
Similar Questions
Knowledge Check
- Question 1 - Select One
The loucs of a point which is a equidistant from two non-intersecting lines l and m is a _____
Astraight line parallel to the line lBStraight line parallel to the line mCStraight line parallel to the line l and m and midway between themDstraight line that intersects both the line l and m - Question 2 - Select One
A part of the locus of a point P, which is equidstant from two intersecting line as+by+c=0andpx+qy+r=0
A(a−p)x+(b−q)y+(c−x)=0Bap+qby+cy=0C√a2+b2(px+qy+r)−√p2+q2(ax+by+a)DNone of these
The locus of the point equidistant from two given points a and b is given by
View SolutionShow that the locus of a point, equidistant from the endpoints of a line segment, is the perpendicular bisector of the segment
View SolutionThe locus of the point in a plane which is equidistant from two intersecting lines is _____
View SolutionProve that the locus of the point equidistant from two given points is the straight line which bisects the line segment joining the given points at right angles.
View SolutionThe set of points joining which are equidistant from any two intersecting lines is called
View SolutionP is a point equidistant from two lines l and m intersecting at point A(see Fig. 7.38). Show that the line AP bisects the angle between them.
View Solution

