Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
Solution
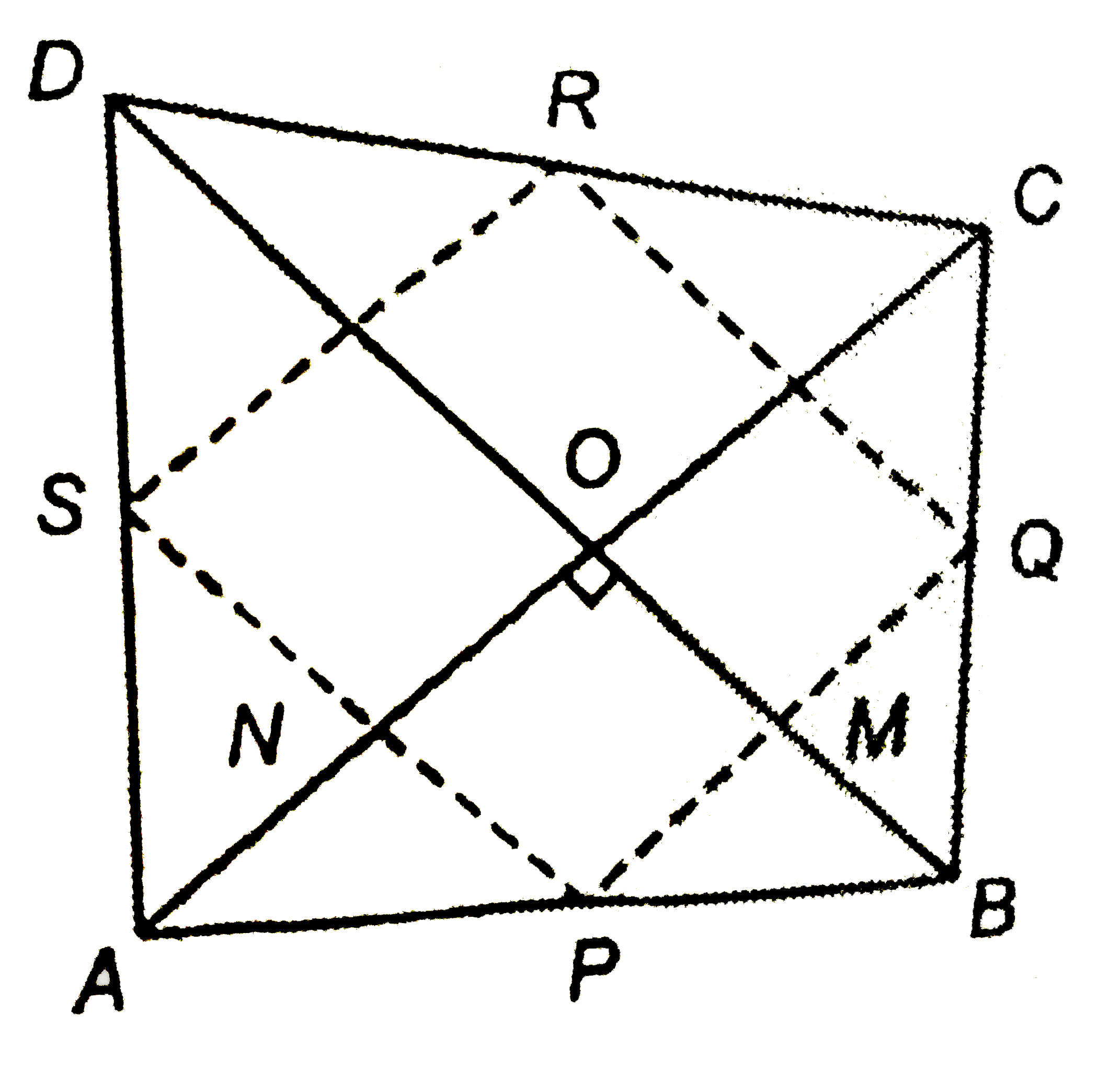
A rectangle ABCD in which P,Q,R and S are the mid-points of sides AB,BC,CD and DA respectively.
PQ,QR,RS and SP are joined
Join AC. In △ABC,P and Q are the mid-points of sides AB and BC = respectively.
∴PQ∣∣AC and PQ=12AC .....(i) (Mid pt. Theorem)
In '△ADC,R' and 'S' are the mid-points of sides CD and AD respectively.
∴'SR∣∣AC' and 'SR= 12
AC ....(ii) (Mid. pt. Theorem)
From (i) and (ii), we have PQ∣∣SR and 'PQ=SR'
⇒'PQRS' is a parallelogram.
Now 'ABCD' is a rectangle.
∴AD=BC
⇒ 12AD=12BC
⇒AS=BQ .....(iii)'
In △S,APS and 'BPQ', we have
AP=BP (P is the mid-point of AB)
∠PAS=∠PBQ (Each is equal to 90∘)
and AS=BQ (From (iii))
∴△APQ≅△BPQ (SAS)
⇒PS=PQ
∴PQRS is a parallelogram whose adjacent sides are equal.
⇒PQRS is a rhombus.
Topper's Solved these Questions
Similar Questions
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrialteral formed by joining the mid-points of the consecutive sides of a rhombus, is a rectangle.
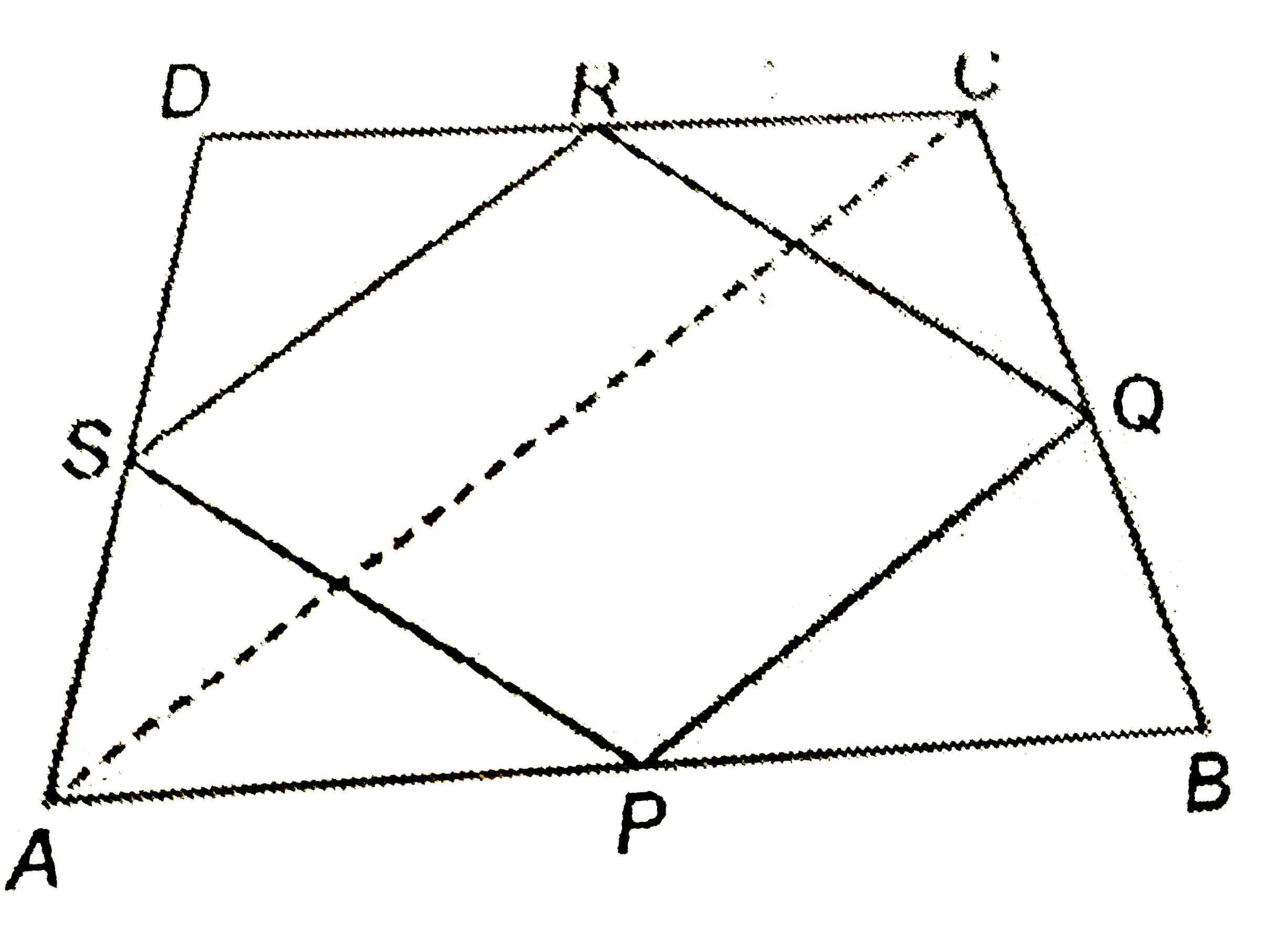
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
 View Solution
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionThe diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionProve that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
 View Solution
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionProve using vectors: The quadrilateral obtained by joining mid points of adjacent sides of a rectangle is a rhombus.
View Solution

