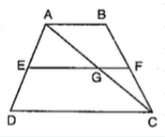
In Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
in ∠ADC
AEED=AMMC
M is the mid point of AC
AB||DC||EF
EF∣∣DC
EM∣∣DC
so,AB∣∣EF
AB∣∣MF
F is also a mid point of BC
as M is the mid point of AD
AMMD=BFFD
EM=12DC
⇒AB∣∣QR
AB=12QR
If A&B are midpoints of PQ & PR
E&M are midpoints
EM∣∣DC&EM=12(DC)
& similarly, MF=12(AB)
EM+MF=12[AB+CD]
EF=12[AB+CD]
hence proved
Topper's Solved these Questions
Similar Questions
In Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
 View Solution
View SolutionIn the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View Solution
Knowledge Check
- Question 1 - Select One
In a trapezium ABCD, AB is parallel to CD. If E is midpoint of side AD and a line drawn from point E, parallel to the parallel sides cuts BC at F then
ABF = CF if AD = BCBBF = CF ia always trueCBF:CF is less than 1 if AD<BCDBF:CF is greater than 1 if AD>BC - Question 2 - Select One
E is the mid-point of the median AD of a ΔABC. If B is extended it meets the side AC at F, then CF is equal to
AAC/3B2AC/3CAC/2DNone of these - Question 3 - Select One
Let ABCD be a trapezium in which AB||DC and E be the mid-point of AD. If F be a point on BC such that EF||AB. Then EF, where F is the mid-point of BC, is equal to
 AAB + DCB12(AB+DC)C13(AB+DC)DNone of these
AAB + DCB12(AB+DC)C13(AB+DC)DNone of these
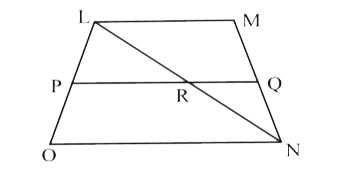
In the figure LMNO, is a trapezium in which LM is parallel to side ON and P is the mid point of side LO. If Q is a point on the side MN such that segment PQ is parallel to side ON Prove that Q is the mid point of MN and PQ=1/2(LM+ON).
 View Solution
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
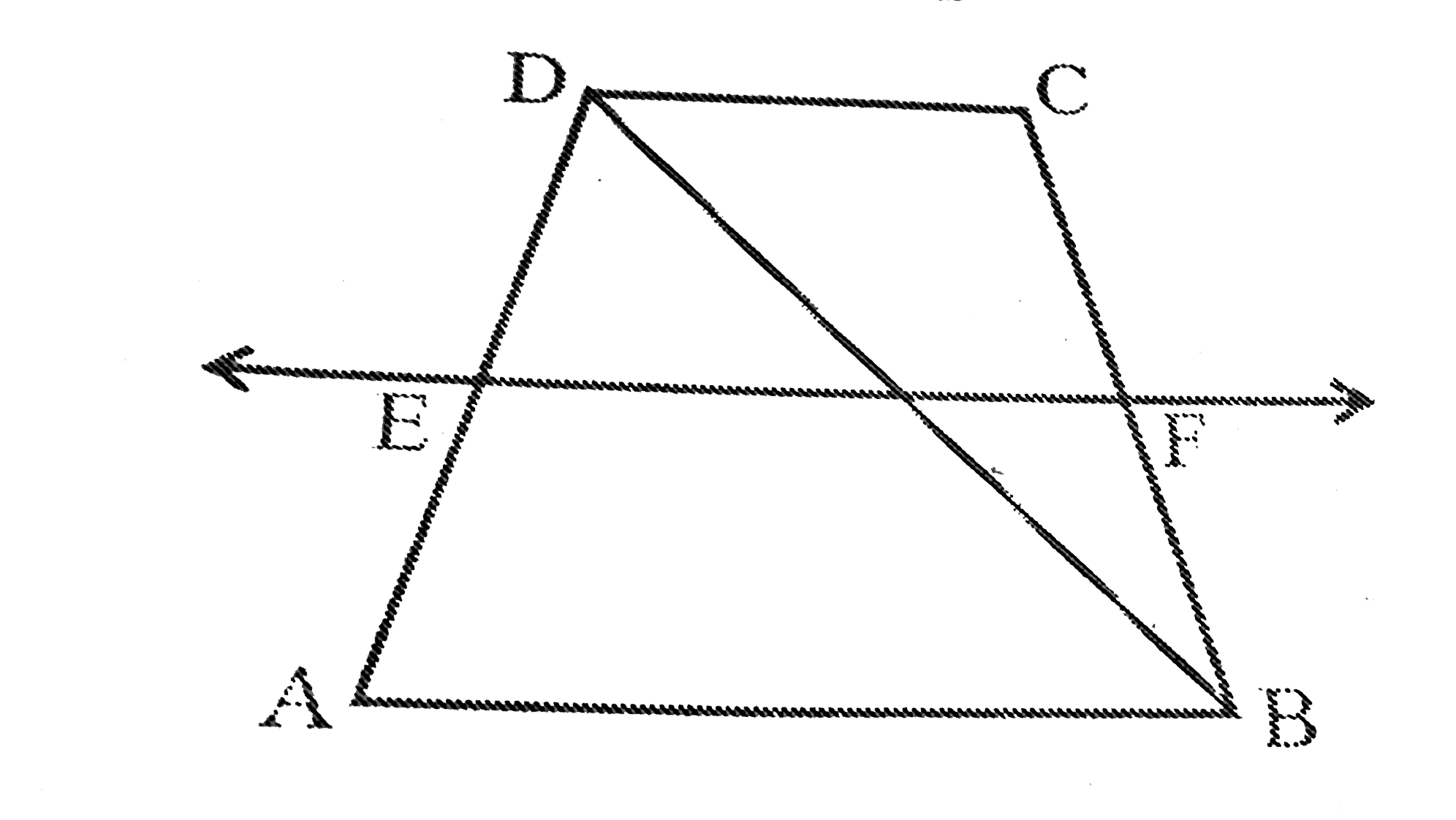
View SolutionABCD is a trapezium in which AB ∣∣ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
 View Solution
View SolutionD is the mid-point of side BC of ABC and E is the mid-point of BD. If O is the mid-point of AE , prove that ar(BOE)=18ar(ABC)
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View Solution

