Show that the relation R defined by
(a,b)R(c,d)⇒a+d=b+c in the set N is an equivalence relation.Solution in Punjabi
Step by step video solution for Show that the relation R defined by (a, b) R(c,d)implies a+d=b+c in the set N is an equivalence relation. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Which one of the following graph represents the function of x? Why?
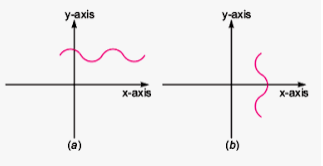 07:05View Solution
07:05View SolutionCompute P(A∣B),if P(B)=0.5 and P(A∩B)=0.32
View SolutionState the reason for the relation R, in the set {1,2,3} given by R= {(1,2), (2, 1), not to be transitive.
03:35View SolutionStatement-1: The relation R on the set N×N defined by (a, b) R (c, d) ⇔ a+d = b+c for all a, b, c, d ∈ N is an equivalence relation.
Statement-2: The intersection of two equivalence relations on a set A is an equivalence relation.05:17View Solutionधनपूर्णांको के समुच्य N में कोई सम्बन्ध R,N×N पर इस प्रकार परिभाषित है, की ---
(a,b)R(c,d)⇒a+d=b+c,(a,b),(c,d)∈N×N
तो सिद्ध कीजिय R तुल्यता सम्बन्ध है ।03:52View SolutionLet R be the relation over the set N×N and is defined by (a,b)R(c,d)⇒a+d=b+c. Then R is :
05:45View SolutionLet N be the set of all natural numbers and let R be a relation on N×N , defined by (a, b)R (c, d)⇔ad=bc for all (a, b), (c, d)∈N×N . Show that R is an equivalence relation on N×N
06:07View SolutionShow that the relation R defined by (a,b)R(c,d)⇒a+d=b+c on the set N×N is an equivalence relation.
09:12View SolutionStatement-1: The relation R on the set N×N defined by (a, b) R (c, d) ⇔ a+d = b+c for all a, b, c, d ∈ N is an equivalence relation.
Statement-2: The intersection of two equivalence relations on a set A is an equivalence relation.07:02View SolutionShow that the relation R on the set N×N defined by (a,b)R(c,d) iff ad(b+c)=bc(a+d) is an equivalence relation.
06:59View SolutionIf N denotes the set of all natural numbers and R be the relation on N×N defined by (a, b) R (c, d) if ad(b+c)=bc(a+d). Show that R is an equivalence relation.
05:43View SolutionStatement-1: The relation R on the set N×N defined by (a, b) R (c, d) ⇔ a+d = b+c for all a, b, c, d ∈ N is an equivalence relation.
Statement-2: The intersection of two equivalence relations on a set A is an equivalence relation.08:41View SolutionLet N denote the set of all natural numbers and R be the relation on NxN defined by (a,b)R(c,d)ad(b+c)=bc(a+d). Check whether R is an equivalence relation on NxN.
05:46View SolutionStatement-1: The relation R on the set N×N defined by (a, b) R (c, d) ⇔ a+d = b+c for all a, b, c, d ∈ N is an equivalence relation.
Statement-2: The intersection of two equivalence relations on a set A is an equivalence relation.04:11View SolutionLet N denote the set of all natural numbers and R be the relation on NxN defined by (a,b)R(c,d)<=>ad(b+c)=bc(a+d). Check whether R is an equivalence relation on N×N.
09:50View SolutionShow that the relation R defined by
(a,b)R(c,d)⇒a+d=b+c in the set N is an equivalence relation.05:30View Solution

