Show that the relation R in the set R of real numbers defined as , is reflexive and transitive but not symmetric.Solution in Punjabi
Step by step video solution for Show that the relation R in the set R of real numbers defined as R = {(a, b) : a le b}, is reflexive and transitive but not symmetric. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Which one of the following graph represents the function of x? Why?
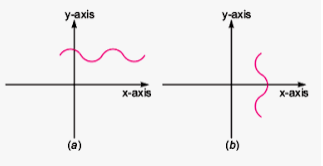 04:24View Solution
04:24View SolutionCompute P(A∣B),if P(B)=0.5 and P(A∩B)=0.32
03:55View SolutionState the reason for the relation R, in the set {1,2,3} given by R= {(1,2), (2, 1), not to be transitive.
03:59View SolutionShow that the relation R in the set R of real numbers, defined as R={(a,b):a≤b2}is neither reflexive nor symmetric nor transitive.
07:00View SolutionShow that the relation R in R defined R={(a,b):a≤b} is reflexive and transitive but not symmetric.
05:35View SolutionShow that the relation R in R (set of real numbers) is defined as R={(a,b),a≤b}is reflexive and transitive but not symmetric.
04:45View SolutionShow that the relation R in the set R of real numbers, defined as
R={(a,b):a≤b2} is neither reflexive nor symmetric nor transitive.05:39View SolutionShow that the relation R in the set R of real numbers, defined as
R={(a,b):a≤b2} is neither reflexive nor symmetric nor transitive.05:17View SolutionShow that the relations R on the set R of all real numbers, defined as R={(a, b):a≤b2} is neither reflexive nor symmetric nor transitive.
05:15View SolutionShow that the relation R in the set R of real numbers, defined as R={(a,b):a≤b2}is neither reflexive nor symmetric nor transitive.
04:44View SolutionShow that the relation R in the set R of real numbers defined as R={(a,b):a≤b}, is reflexive and transitive but not symmetric.
03:01View SolutionShow that the relation R in the set R of real numbers defined as R=((a,b):a≤b}, is reflexive and transitive but not symmetric.
06:08View SolutionShow that the relation R in the set R of real number , defined as R={(a,b):a≤b2} is neither reflexive nor symmetric nor transitive.
06:45View SolutionShow that the relation R is R defined as R={(a,b):a≤b} is reflexive and transitive but not symmetric.
02:39View SolutionShow that the relation R in R (Set of real numbers) is defined as R={(a,b):a≤b} is reflexive and transitive but not symmetric.
04:59View SolutionShow that the relation R in the set R of real numbers, defined as R={(a,b):a≤b2}, is neither reflexive nor symmetric nor transitive.
05:20View Solution

