Show that zero is the identity for addition on R and 1 is the identity for multiplication on R. But there is no identity element for the operations ÷R×R→R and ÷:R⋅×R⋅→R⋅.
We know that a+0=a=0+a and a×1=a=1×a∀a∈R
⇒ 0 is the additive identity and 1 is the multiplicative identity in R.
Now ,there is no element e in R such that
a−e=a=e−a∀a∈R
∴ For −:R×R→R, there is no identity element in R.
Similarly, for ÷:R×R→R, there is no identity element in R.
Hence Proved.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONS Book:NAGEEN PRAKASHANChapter:RELATIONS AND FUNCTIONS Exercise:Exercies 1a
Explore 16 Videos
- RELATIONS AND FUNCTIONS Book:NAGEEN PRAKASHANChapter:RELATIONS AND FUNCTIONS Exercise:Exercies 1b
Explore 18 Videos
- PROBABIILITYBook:NAGEEN PRAKASHANChapter:PROBABIILITYExercise:Miscellaneous Exercise
Explore 19 Videos
- THREE-DIMENSIONAL GEOMETRY Book:NAGEEN PRAKASHANChapter:THREE-DIMENSIONAL GEOMETRY Exercise:Miscellaneous Exercise
Explore 23 Videos
Similar Questions
Show that zero is the identity for addition on R and 1 is the identity for multiplication on R. But there is no identity element for the operations −:R×R→Rand ÷:R⋅×R⋅→R⋅.
View SolutionShow that – a is the inverse of a for the addition operation '+' on R and 1a is the inverse of a≠0for the multiplication operation X on R.
View Solution
Knowledge Check
Identity P,Q,R and S in the diagram
 AP-negative regative, Q-inhibitor,R-effector molecule, S-positive regulationBP-positive regulation, Q-effector molecule, R-inhibitor,S-negative regulationCP-negative regulation, Q-inhibitor, R-positive regulation, S-effector moleculeDP-positive regulative, Q-effector molecule,R-negative regulation, Sinhibitor.
AP-negative regative, Q-inhibitor,R-effector molecule, S-positive regulationBP-positive regulation, Q-effector molecule, R-inhibitor,S-negative regulationCP-negative regulation, Q-inhibitor, R-positive regulation, S-effector moleculeDP-positive regulative, Q-effector molecule,R-negative regulation, Sinhibitor.Let '∗' be the binary operation defined on the set Z of all integers as a∗b=a+b+1 for all a, b ∈Z. The identity element w.r.t. this operations is
A−1B−2C1D0
Let R be a reflexive relation on a set A and I be the identity relation on A. Then
View SolutionWhat is the identity element with respect to multiplication?
View SolutionIf * defined on the set R of real numbers by a⋅b=3ab7 , find the identity element in R for the binary operation *.
View SolutionIdentity A, B, C, D, E, R and R' in the following:
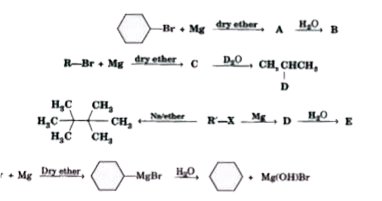
View SolutionIdentity A, B, C, D, E, R and R' in the following:

View SolutionIf ∗ is a binary operation on the set R of all real numers difined by a∗b=a+b−3 then find the identity element for ∗.
View Solution
