Identity A, B, C, D, E, R and R' in the following:
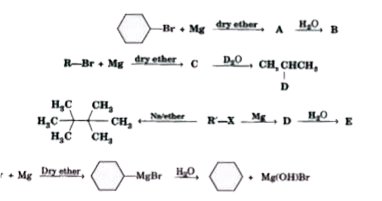
R−Br+MgDry ether−−−−−→RMgBr(C)D2O−−→CH3C∣DHCH3
Since D geta attached to mame C-atom on which MgBr or Br was present so that
R−Br:CH3Br∣CHCH3 or R:CH3−H∣CH−CH3 and C:CH3−C∣CH3H−MgBr
Tert-alkyl halidea donot undergo Wurtz reaction. Therefore, the question is not correct. They undergo dehydrohalogenation to give alienes. Hence, R.=(CH3)3CH
CH3−CH3∣C=CH3Na,ether←−−−−−−HBrCH3−CH3∣C∣CH3−Brtert-butylbromide(R.Br)Mg−−→CH3−CH3∣C∣CH3−MgBr(D)H2O−−→CH3−CH3∣C∣CH3−H2-Methylpropane
Topper's Solved these Questions
- HALOALKANES AND HALOARENESBOOK - MODERN PUBLICATIONCHAPTER - HALOALKANES AND HALOARENESEXERCISE - NCERT Textbooks Exercises
1 Videos
- HALOALKANES AND HALOARENESBOOK - MODERN PUBLICATIONCHAPTER - HALOALKANES AND HALOARENESEXERCISE - NCERT Textbooks Exercise
21 Videos
- HALOALKANES AND HALOARENESBOOK - MODERN PUBLICATIONCHAPTER - HALOALKANES AND HALOARENESEXERCISE - CONCEPTUAL QUESTIONS
25 Videos
- EQUILIBRIUMBOOK - MODERN PUBLICATIONCHAPTER - EQUILIBRIUMEXERCISE - Unit Practice Test
13 Videos
- HYDROCARBONSBOOK - MODERN PUBLICATIONCHAPTER - HYDROCARBONSEXERCISE - UNIT PRACTICE TEST
15 Videos
Similar Questions

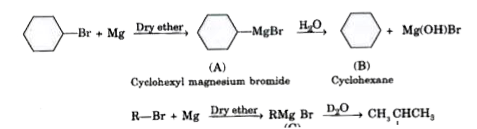
Identify A, B, C, D, E, R and R' in the following:
View SolutionIdentify A, B, C, D, E, R and R1 in the following:
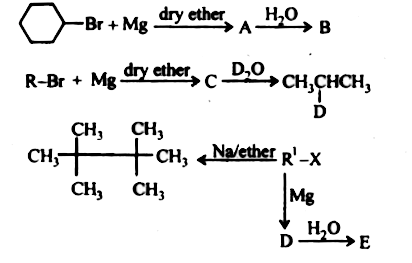
View SolutionIdentify A, B, C, D, E, R and R1 in the following:

View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: ar (ACB)=ar (ACF) ar (AEDF)=ar (ABCDE)
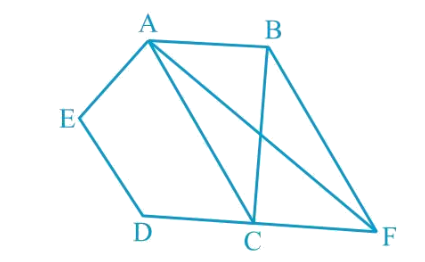
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that ar(ACB)=ar(ACF) (ii) ar(AEDF)=ar(ABCDE)
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: (i) ar(△ACB)=ar(△ACF) (ii) ar(quadrilateralAEDF)=ar(ABCDE)
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that:
(i) ar (ACB)=ar (ACF)
(ii) ar (AEDF)=ar (ABCDE)
View SolutionIn triangle ABC , if AD is the bisector of ∠A , prove that: Area(ABD)Area(ACD)=ABAC
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that : ar(ADEG)=ar(GBCE) ar(EGB)=16ar(ABCD)
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(△ADF)=ar(△DCE).
View Solution
