Sides of a triangular field are 15 m, 16m and 17m. With the three corners of the field a cow, a buffalo and a horse are tied separately with ropes of length 7m each to graze in the field. Find the area of the field which cannot be grazed by the three animals.
Since with the three corners of the field a cow, a buffalo and a horse and tied separately with rope of length 7m each to graze in the field.
Area of field which cannot be grazed by animals = Area of ΔBCA− Area of three sectors
Here, a=15m,b=16m,c=17m
∴s=a+b+c2=15+16+172
⇒s=482=24cm
Area of ΔBCA=√s(s−a)(s−b)(s−c)
=√24(24−15)(24−16)(24−17)
=√24×9×8×7
=√2×2––––––×2–×3×3×3––––––×2–×2×2––––––×7
⇒ar(ΔBCA)=24√21m2
Area of 3 secotrs =πr2θ1360∘+πr2θ2360∘+πr2θ3360∘
=πr2360∘(θ1+θ2+θ3)
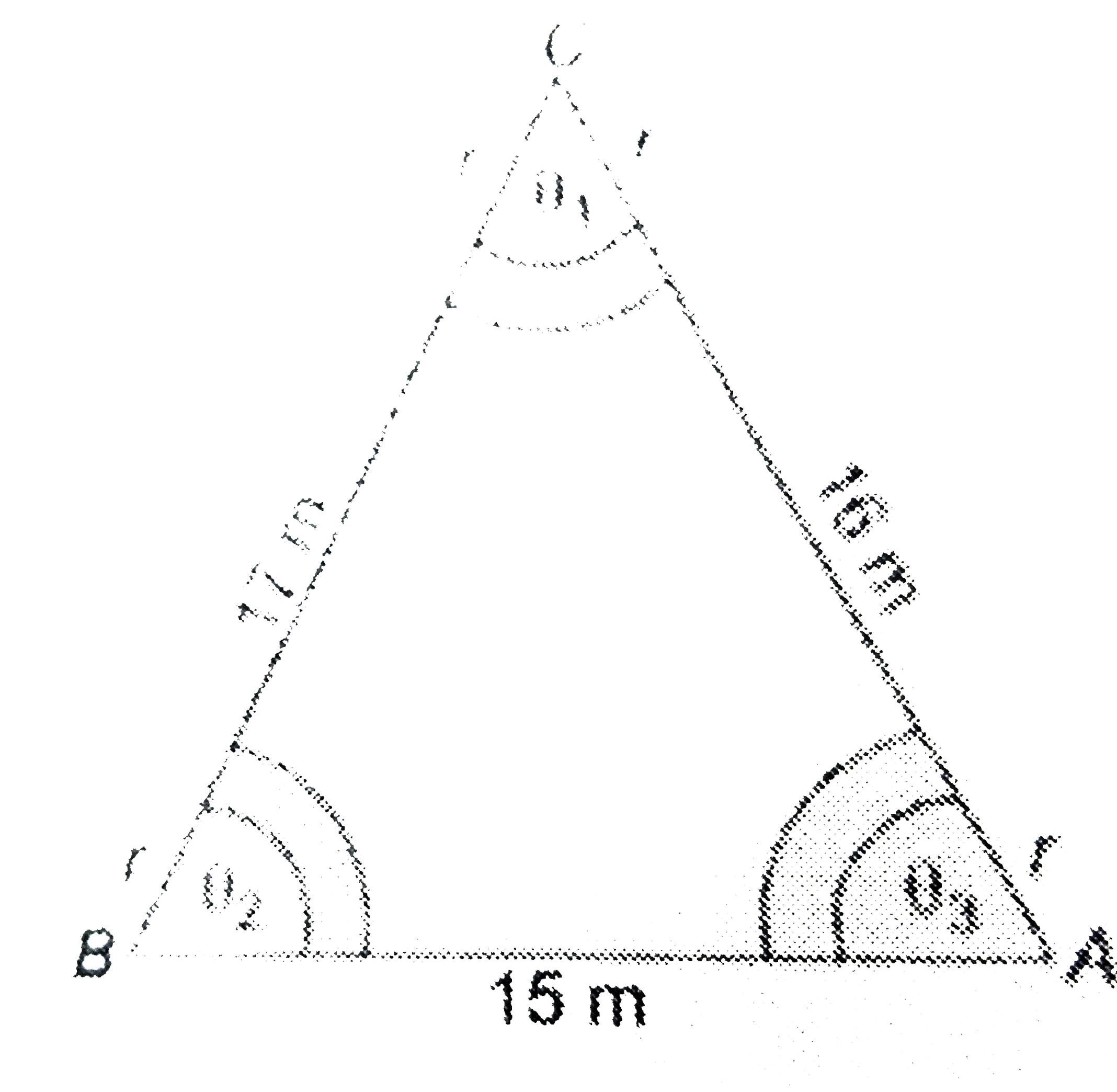
=227×7×7360∘×180∘(∴θ1+θ2+θ3=180∘)
∴ Area of 3 sectors grazed by animals =77m2
Hence, the area which cannot be grazed by 3 animals is equal to (24√21−77)m2
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 A
24 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 B
32 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Revision Exercise Long Answer Question
5 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
Similar Questions
Sides of a right triangular field are 25m, 24m and 7m. At the three corners of the field, a cow, a buffalo and a horse are tied separately with ropes of 3.5 m each to graze in the field. Find the area of the field that cannot be grazed by these animals.
View SolutionA rectangular field is of length 60 m and breadth 35 m. Find the area of the field.
View SolutionA cow is tied with a rope of length 14m at the corner of a rectangular field of dimensions 20m×16m . Find the area of the field in which the cow can graze.
View SolutionThe perimeter of a triangular field is 144 m and the ratio of the sides is 3:4:5. Find the area of the field.
View SolutionThere is a rectangular field of size 94 m×32 m. Three roads each of 2 m width pass through the field such that two roads are parallel to the breadth of the field and the third is parallel to the length. Calculate: (a) Area of the field covered by the three roads (b) Area of the field not covered by the roads.
View SolutionThe perimeter of a triangular field is 540m and its sides are in the ratio 25:17:12. Find the area of the triangle.
View SolutionA rectangular field is 112 m long and 62 m broad. A cubical tank of edge 6 m is dug at each of the four corners of the field and the earth so removed is evenly spread on the remaining field. Find the rise in level.
View SolutionA rectangular field is 112m long and 62m broad. A cubical tank of edge 6m is dug at each of the four corners of the field and the earth so removed is evenly spread on the remaining field. Find the rise in level.
View SolutionLength and breadth of a rectangular field are 50 m and 15 mrespectively. Find the ratio of the length to the breadth of the field.
View SolutionFind the area of a square field if its each side is 1034 m long.
View Solution
