Sketch the origin in which the points satisfying the following inequalities lie.
(i)|x+y|<2 (ii) |2x−y|>3 (iii) |x|>|y|Solution in Bengali
(i)|x+y|<2
∴−2<x+y<2
⇒x+y+2>0andx+y−2<0
L1(x,y)=x+y+2 and L2(x,y)=x+y−2
L1(0,0)=2>0 andL2(0,0)=−2<0
So ,x+y+2>0 represents the region where origin lies and x+y−2<0 also represents the region where origin lies.
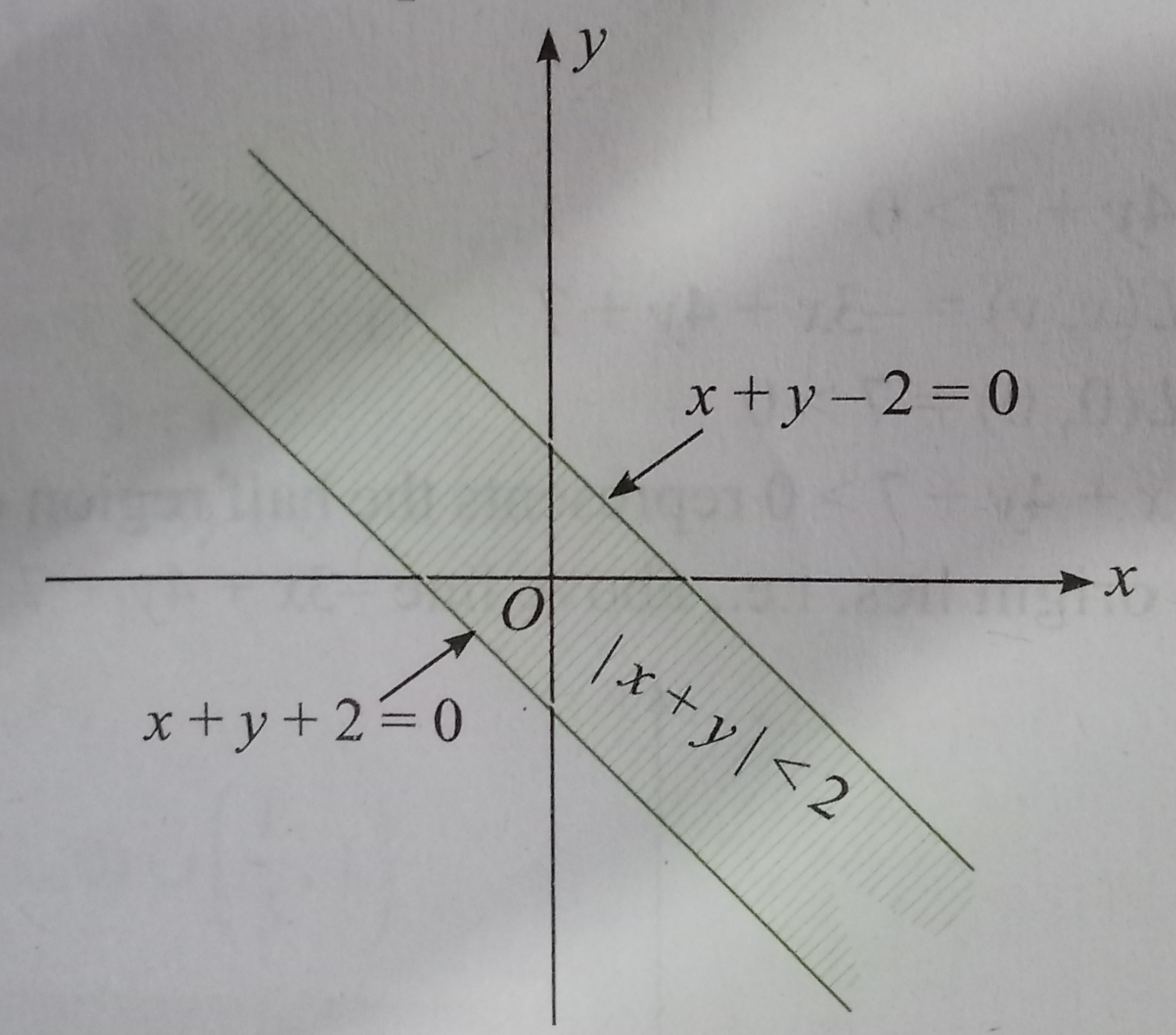
Thus, in general, |ax+by+c|<d is the region of the points
between the lines ax+by+c =d and ax+by+c = -d.
(ii)|2x−y|>3
∴2x−y<−3 and 2x−y>3
⇒2x−y+3<0 and 2x−y−3>0
L1(x,y)=2x−y+3 and L2(x,y)=2x−y−3
L1(0,0)=1>0 and L2(0,0)=−3<0
So, 2x−y+3<0 represents where origin doest not lie and 2x−y−3>0 also represents the region where origin does not lie.
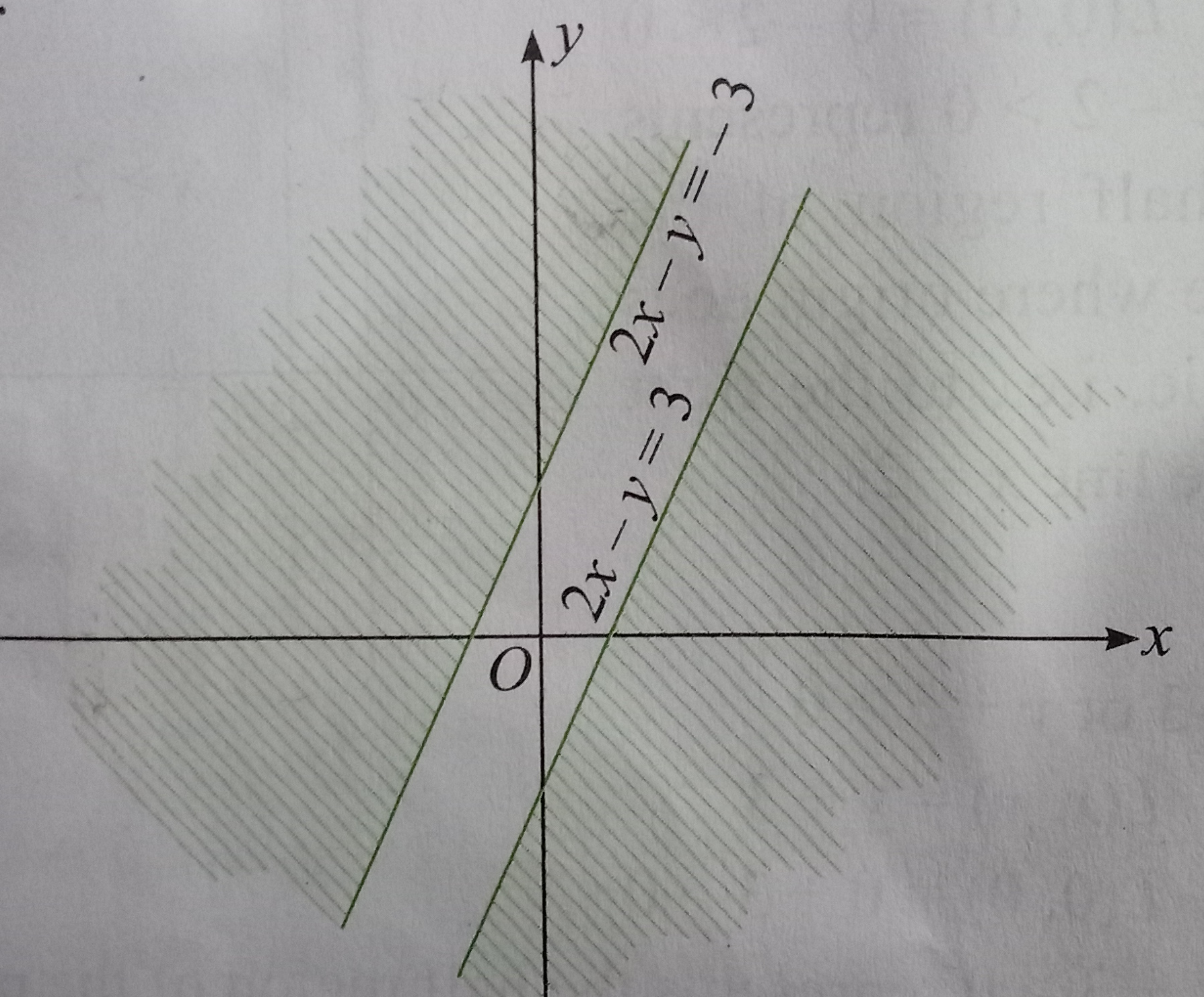
Thus, in general |ax+by+c|>d is the region of the points which does not lie between the lines ax+by+c =d and ax+by+c=-d.
(iii)|x|>|y|
If x,y>0, then we have x>y orx−y>0.
Let L(x,y) = x-y.
∴L(1,0)=1−0>0.
Hence, points satisfying this inequality lie below the line x-y=0 in first quadrant.
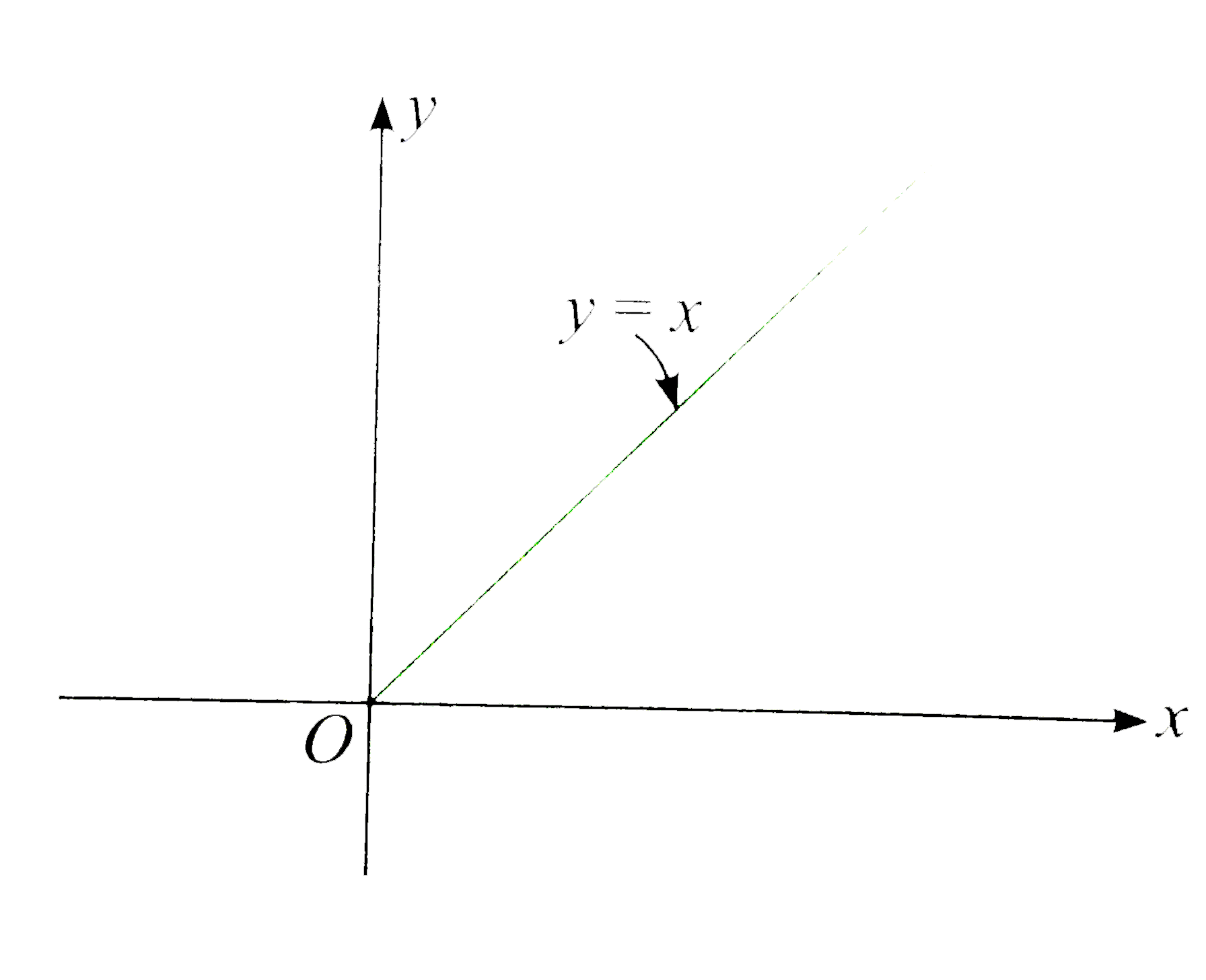

Ifx>0,y>0, then we have x>−y orx+y>0.
Let L(x,y) = x+y.
∴L(1,0)=1+0>0
Points satisfying this inequality lie above the line x+y=0 in fourth quadrant.
Similarly, we have one region in second quadrant and one in third quadant.
Combining all the cases, we have following region.
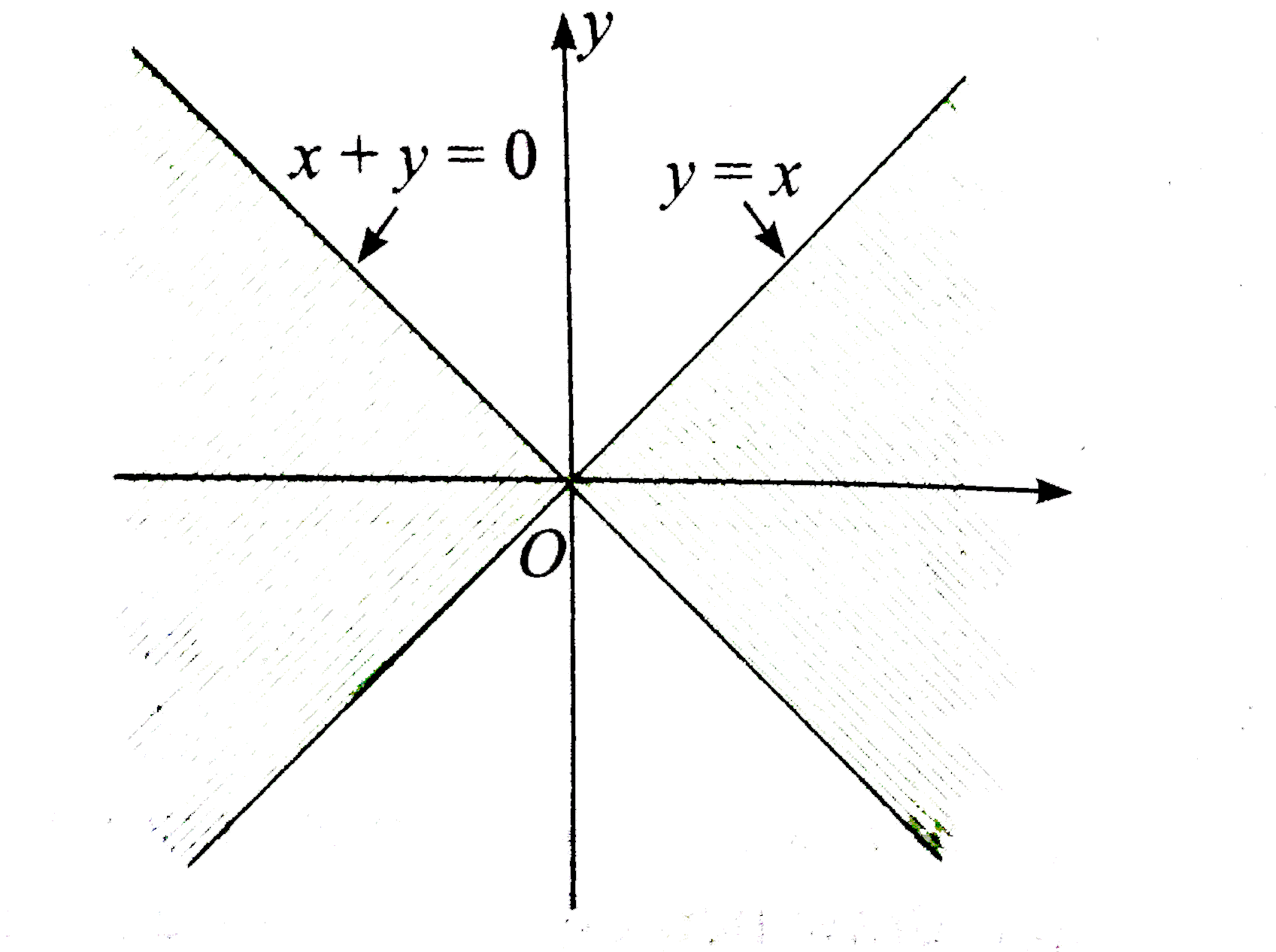
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE
12 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.1
23 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
Show that the lines 4x+y−9=0,x−2y+3=0,5x−y−6=0 make equal intercepts on any line of slope 2.
View SolutionFind the equation of the right bisector of the line segment joining the points (3,4) and (-1,2).
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionSketch the regions satisfying the following inequalities:
(a) x>2
(b) |y|≥1
View SolutionSketch the origin in which the points satisfying the following inequality lie.
(i)2x−3y−5>0 (ii) −3x+4y+7>0
(iii)x>2 (iv) y>−3
View SolutionSketch the origin in which the points satisfying the following inequalities lie.
(i)|x+y|<2 (ii) |2x−y|>3 (iii) |x|>|y|
View SolutionIf (x,y) represents a point and |x|>0 and y<0 , then in which quadrant(s) can the point lie ?
View SolutionFor all nonzero numbers x and y, the operation ∇ is defined by the equation x∇y=|x|x2+y2|y| when x>y and by the equation x∇y=|x|y2−x2|y| when x≤y. If x∇y<0, then which of the following could be true ?
I. x3=y3
II. (y+x)(y−x)>0
III. x−y>0
View Solutiony>2x−1
2x>5
Which of the following consists of the y-coordinates of all the points that satisfy the system of inequalities above?
View SolutionSketch the regions satisfying the following inequalities:
(a) x>2
(b) |y|≥1
View SolutionSketch the origin in which the points satisfying the following inequality lie.
(i)2x−3y−5>0 (ii) −3x+4y+7>0
(iii)x>2 (iv) y>−3
View SolutionSketch the origin in which the points satisfying the following inequalities lie.
(i)|x+y|<2 (ii) |2x−y|>3 (iii) |x|>|y|
View SolutionSolve the following systems of linear inequalities graphically : x+y>1,3x−y<3,x−3y+3>0.
View SolutionSolve the following systems of linear inequalities graphically : x>y,x<1,y>0.
View Solution
