Question

Solve the following LPP by using graphical method.
Maximize : ${\displaystyle Z=6x+4y,}$
Subject to ${\displaystyle x\le 2,x+y\le 2,-2x+y\le 1,x\ge 0,y\ge 0.}$ Also find maximum value of Z.

Explanation

Maximum : `z=6x+4y`
Subject to `x le 2, x +y le 2, - 2x+yle 1, x ge 0 ` and `y ge 0`.
Now,

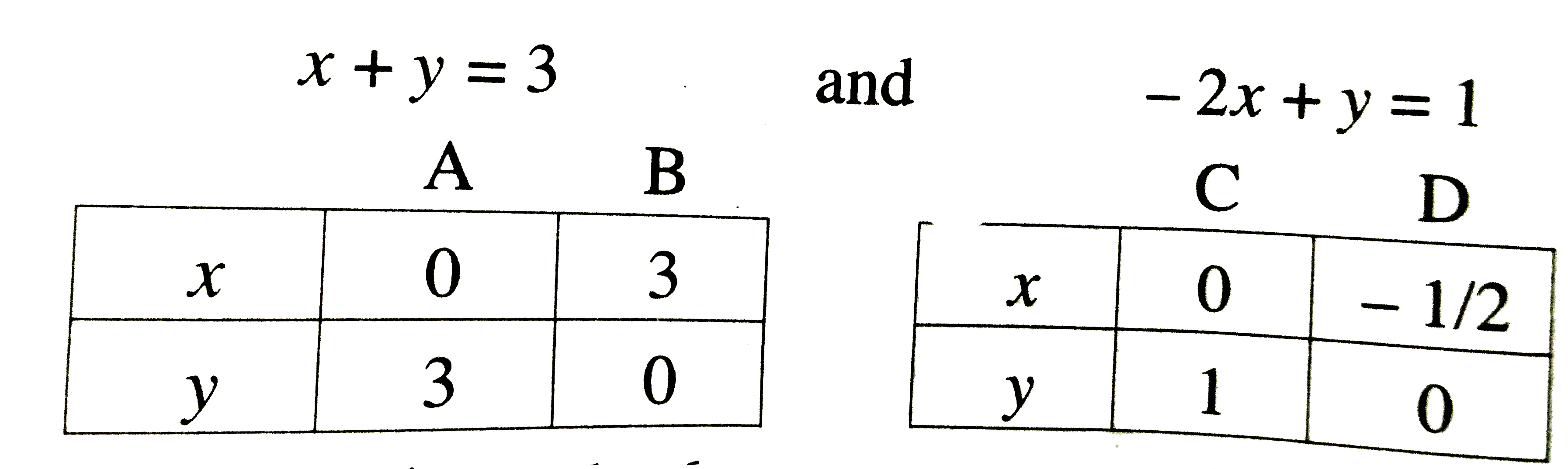
First we draw the lines AB, CD and RS whose equations are `x=2, x+y=3` and `-2x+y=1` respectively.

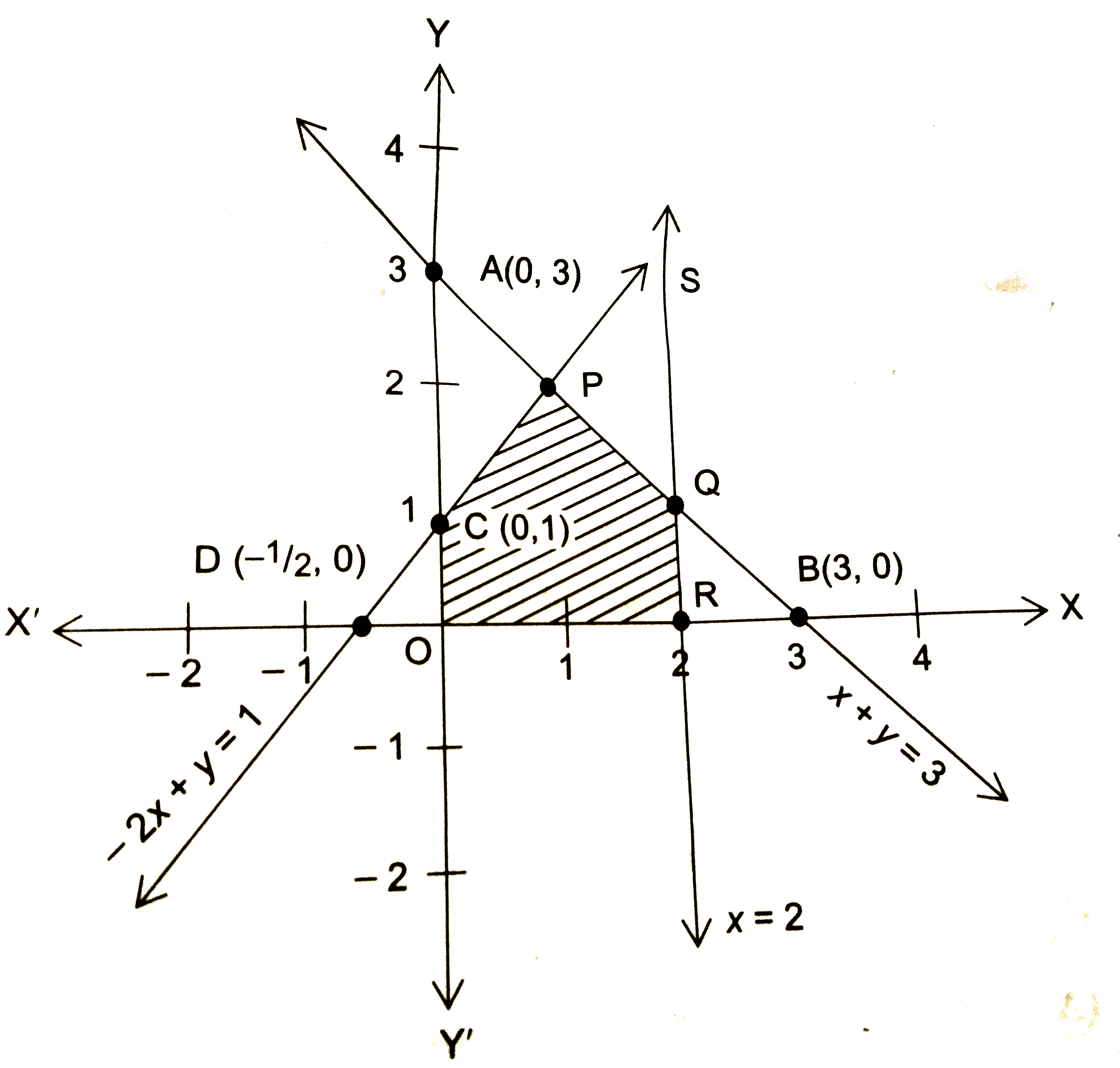
The feasible region is ORQPCO which is shaded in the figure. The vertices of the feasible region are O `(0,0), R(2,0) Q,P` and `C(0,1)`.
P is the point of intersection of the lines `x+y=3`
and `-2x+y=1`
Solving these equations we get point `P(2//3, 3//7)`.
Q is the point of intersection of the lines `x+y=3` and x = 2
Putting x = 2 in `x+y=3,` we get y = 1
Point Q(2,1) Putting x = 2 in `x+y=3`, we get y = 1
Point Q (2, 1)
The value of the objective function `z=6x+4y` at these vertices are

`therefore ` The maximum value of z is 16, when x = 2 and y = 1.