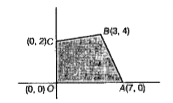
Solve the following LPP graphically Optimize Z=5x1+25x2 subject to −0.5x1+x2≤2,x1+x2≥2,−x1+5x2≥5,x1,x2≥0Solution in Odia
The correct Answer is:Hence, Z has minimum at A =(56,76) and has no maximum value.
Step by step video, text & image solution for Solve the following LPP graphically Optimize Z=5x_1+25x_2 subject to -0.5x_1+x_2 le 2, x_1+x_2 ge 2, -x_1+5x_2 ge 5, x_1, x_2 ge 0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - CHAPTER PRACTICE (Short Answer Type Questions 4 Marks)11videos
LINEAR PROGRAMMING
- BOOK - ARIHANT PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - CHAPTER PRACTICE (Long Answer Type Questions 6 Marks)18videos
LINEAR PROGRAMMING
- BOOK - ARIHANT PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - ODISHA BUREAU.S TEXTBOOK SOLUTIONS (Exercise 3(a))11videos
LINEAR PROGRAMMING
- BOOK - ARIHANT PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - CHAPTER PRACTICE35videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - ARIHANT PUBLICATIONCHAPTER - MATRICES EXERCISE - CHAPTER PRACTICE (Very Short Answer Type Questions)56videos
MATRICES
Similar Questions
Feasible region (shaded) for an LPP is shown in the following figure, Maximise Z = 5x + 7y
 02:55View Solution
02:55View SolutionFind the maximum and minimum value of 2x + y subjects to the constraints are
x+3y≥6,x−3y≤3,3x+4y≤24
−3x+2y≤6,5x+y≥5 and x,y≥001:30View SolutionA merchant sells two models X and Y of TV with cost price ₹ 25000 and ₹ 50000 Per set respectively. He gets a profit of ₹ 1500 on model X and ₹ 2000 on model Y . The sales connot exceed 20 sets in a month. If he cannot invest more than 6 lakh rupees, formulate the problem of determining the number of sets of each type he must keep in stock for maximum profit.
01:34View SolutionEvaluate cot−1(−√3).
10:35View SolutionWhat possible orders of a matrix can have , if it has
(i) 5 elements ?
(ii) 8 elements ?04:06View Solutionx1+x2≥3,2x1+5x2≤10,x1,x2≤0 के व्यापक हल में निम्न में से कौन-सा बिन्दु स्थित होगा :
04:06View SolutionBy graphical method, the solutions of linear programming problem maximum Z=3x1+5x2 subject to constraints 3x1+2x2≤18
x1≤4,x2≤6,x1≥0,x2≥004:56View SolutionFor the LPP, Min Z=x1+x2 such that inequalities 5x1+10x2≥0,+x2≤1,x2≤4 and x1,x2≥0
10:35View SolutionSolve the following LPP graphically Optimize Z=5x1+25x2 subject to −0.5x1+x2≤2,x1+x2≥2,−x1+5x2≥5,x1,x2≥0
04:13View SolutionOptimize :Z=5x1+25x2
Subject to:−0.5x1+x2≤2
−x1+5x2≥5
x1,x2≥0View SolutionMaximize :Z=20x1+40x2
Subject to:x1+x2≤1
x1,x2≥0.10:25View SolutionMinimize:Z=6x1+7x2
Subject to:x1+2x2≥4
x1,x2≥004:13View SolutionSolve the following LPP graphically Optimize Z=5x1+25x2 subject to −0.5x1+x2≤2,x1+x2≥2,−x1+5x2≥5,x1,x2≥0
10:42View SolutionSole the following LPP graphically
Maximise Z=6x1+7x2
Subject to x1+2x2≥2,x1,x2≥0.View SolutionSolve the following LPP graphically.
Maximize Z=4x1+3x2
Subject to x1+x2≤50
x12x2≤80,2x1+x2≥20 and x1,x2≥0View SolutionSolve the following LPP graphically Maximize z=5x1+3x2
Subject to 3x1+5x2≤15<br>,5x1+2x2≤10<br>,x1,x2≥0.14:47View Solution
