Doubtnut Promotions Sticky

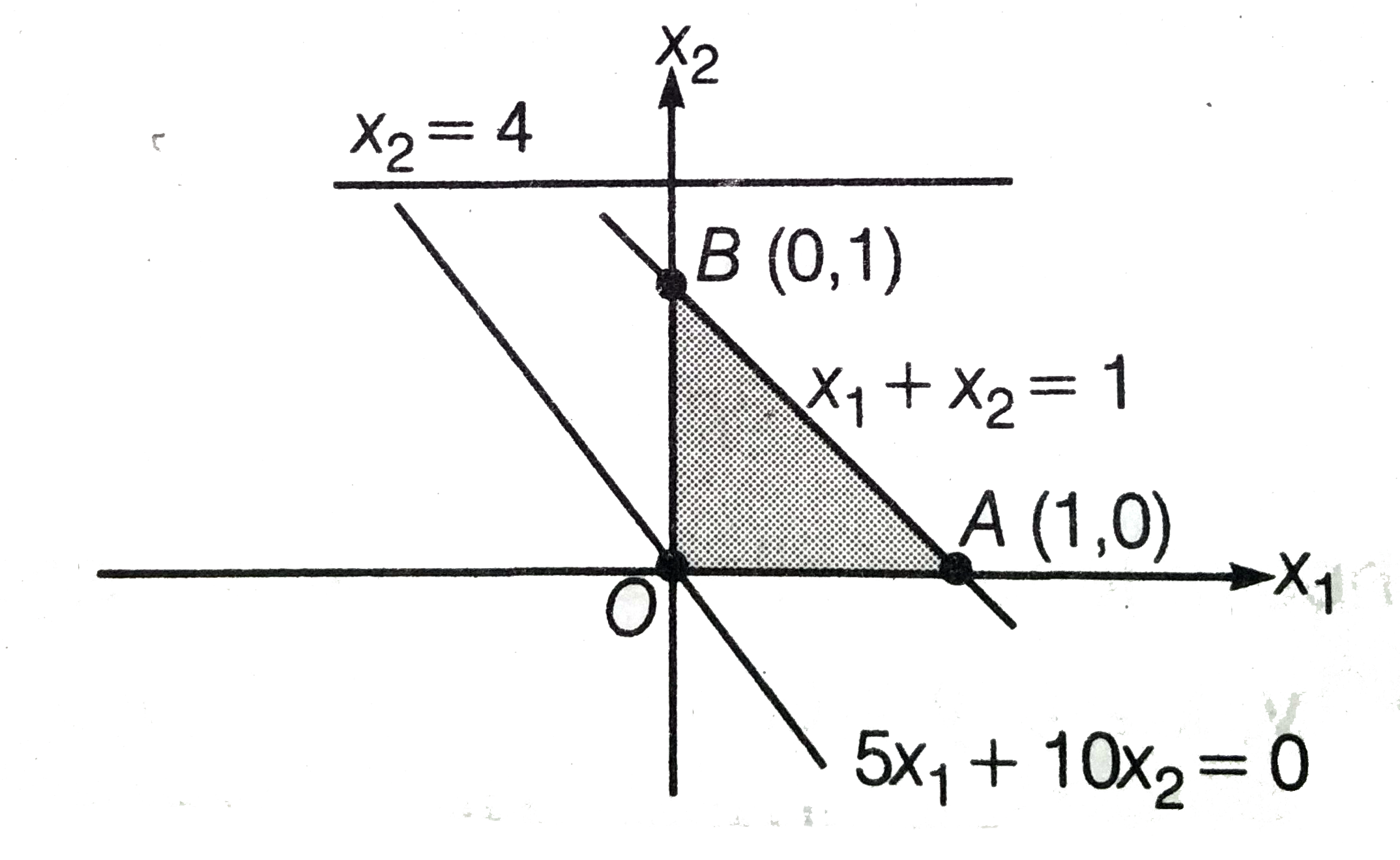
For the LPP, Min Z=x1+x2 such that inequalities 5x1+10x2≥0,+x2≤1,x2≤4 and x1,x2≥0

A

There is a bounded solution

B

There is no solution

C

There are infinite solutions

D

None of the above

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

It is clear from the graph that it clear from the graph that it is bounded solution .
ocr_image

|
Updated on:21/07/2023
Class 12MATHSLINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    For the LPP Min z=x1+x2 such that inequalities
    5x1+10x2≥0,x1+x2≤1,x2≤4 and x−1,x2≥0

    AThere is a baunded solution
    BThereis no solution
    CThere are infinite solutions
    DNone of the above
  • Question 2 - Select One

    By graphical method, the solutions of linear programming problem maximum Z=3x1+5x2 subject to constraints 3x1+2x2≤18
    x1≤4,x2≤6,x1≥0,x2≥0

    Ax1=2,x2=6,Z=36
    Bx1=2,x2=6,Z=36
    Cx1=4,x2=3,Z=27
    Dx1=4,x2=6,Z=42
  • Question 3 - Select One

    The minimum vlaue Z=2x1+3x2 subject to the conditions 2x1+7x2≥22,x1+x2≥6,5x1+x2≥10 and x1,x2≥0 is

    A14
    B20
    C10
    D16