Solve the following problem graphically:Minimise and Maximise $Z = 3 x + 9 y$ . . . (1)subject to the constraints: $x + 3 y \leq 60$ . . . (2) $x + y \geq 10$ . . . (3) $x \leq y$ . . . (4) $x \geq 0, y \geq 0$ . . . (5)

Video Solution

Text Solution

Verified by Experts

Let $Z = 3 x + 9 y$ ....(1)
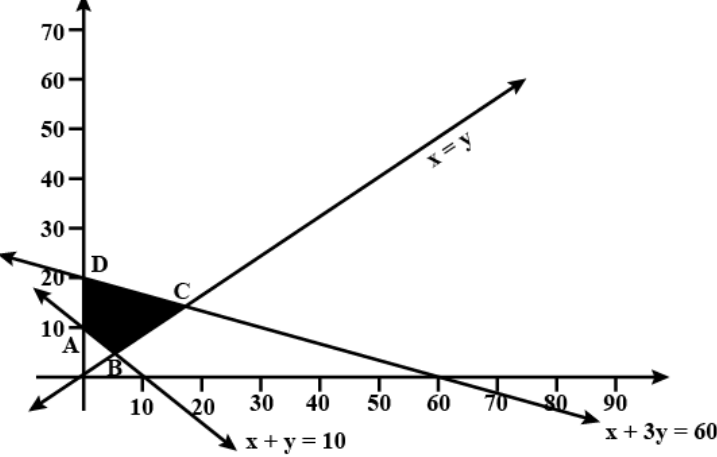
Converting inequalities to equalities $x + 3 y = 60$ to solve these equation we get the required points are $(0, 20), (60, 0)$
$x + y = 10$ we get required points are $(0, 10), (10, 0)$
and $x - y = 0$ we get required points are $(0, 0), (10, 10), (20, 20)$
Plot the graph for the set of points
The graph shows the bounded feasible region. $A B C D$ , with corner points $A = (10, 0), B = (5, 5), C = (15, 15)$ and $D = (0, 20)$ To find maximum and minimum
$⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ \begin{matrix} Corner point & Z = 3 x + 9 y A = (0, 10) & 90 B = (5, 5) & 60 C = (15, 15) & 180 D = (0, 20) & 180 \end{matrix} ⎤ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦$
From the graph maximum value of X occurs at two corner points $C (15, 5)$ and $D (0, 20)$ with value 180 and minimum occurs at point $B (5, 5)$ with value $60 .$

Updated on:21/07/2023