(Manufacturing problem) A manufacturer has three machines I, II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine HI must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the use of all the three machines. The number of hours required for producing 1 unit of each of M and N on the three machines are given m the following table:She makes a profit of Rs 600 and Rs 400 on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?
M= x -> 600x
N= y -> 400y
Z=600x+400y
x≥0
y≥0
x+2y≤12 M1
2x+y≤12 M2
x+54y≥5 M3
BY PLOTTING GRAPHICAL POINTS we get
A[0,6]=2400
B[0,4]=1600
C[4,4]=4000
D[6,0]=3600
E[5,0]=3000
so max value is at , x=4;y=4
Answer
Similar Questions
A manufacturer has three machines A,B and C installed in his factory. Machines A and B are capable of being operated for atmost 12 hours whereas machine C must be operated for atleast 5 hours a day. He produces only two items X and Y each requiring the use of all the three machines. The number of hours required for producing 1 unit of each of X and Y on three machines are given in the following table:
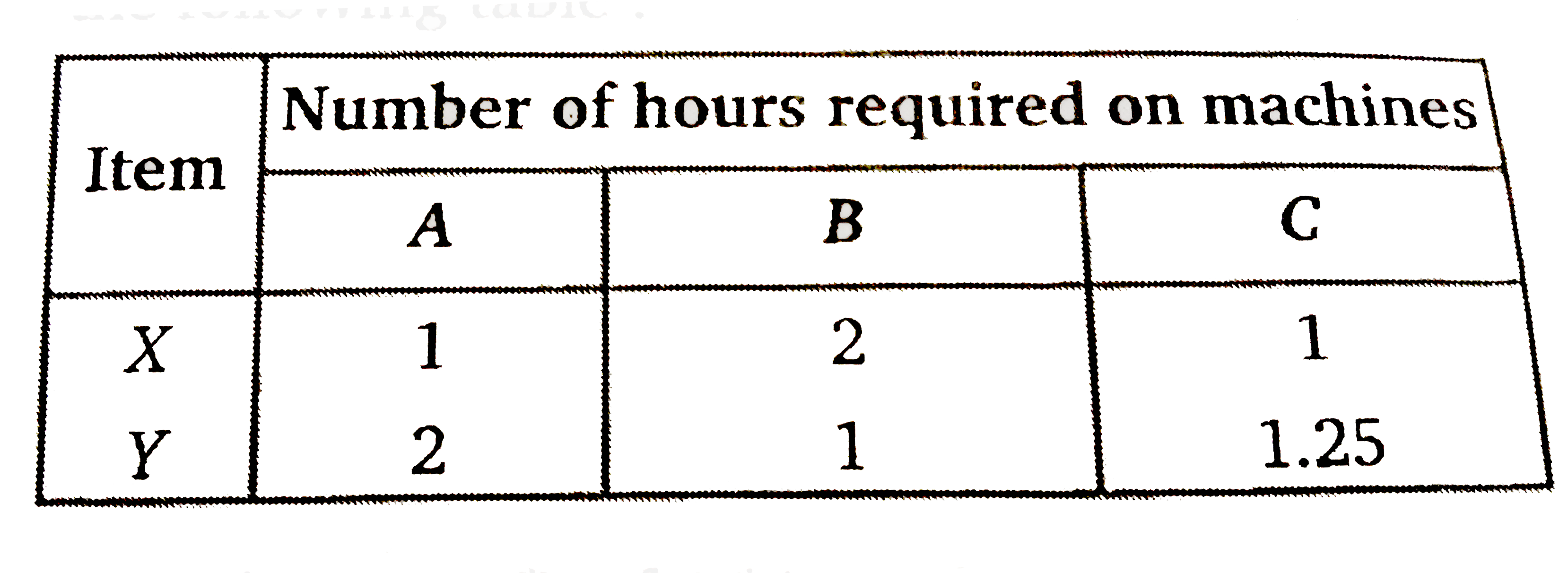
He makes a profit of Rs. 600 and Rs. 400 on each item of X and Y respectively. How many of each item should he produce so as to maximize his profit assuming that he can sell all the items that he produced?View SolutionFind three machines that can be replaced with hook ups of (×5) machines.
View Solution
Knowledge Check
- Question 1 - Select One

What is the least number of machine hours required to produce 30 pieces of P and 25 pieces of Q?A6 hours 30 minutesB7 hours 24 minutesC5 hours 48 minutesD4 hours 6 minutes - Question 2 - Select One
A company produces three products. The products are processed on 3 different machines. The time required to manufacture one unit of each the three products and the daily capacity of three machines are given in the table below :

How many units of product 1 can be produced in one day?AA. 160BB. 205CC. 225DD. 64
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rsl7.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
View SolutionA manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs. 17.50 per package on nuts and Rs. 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
View SolutionA cottage industry manufactures pedestal lamps and wooden shades.Both the products require machine time as well as craftsman time in the making.The number of hours required for producing 1 unit of each and the corresponding profit is given in the following table:
In a day,the factory has availability of not more than 42 hours of machine time and 24 hours of craftsman time.
Assuming that all items manufactured are sold,how should the manufacturer schedule his daily production in order to maximise the profit?Formulate it as an LPP and solve it graphicallyView SolutionMachine A can produce 6 items per hour and machine B can produce 11 items per hours. If machine A works for x hours and B works for y hours in a day and both the machines produce at the most 200 items in a day, then frame an inequation to support the above data.
View SolutionA manufacturer produces nuts and bolts. It takes 2 hours work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 2 hours on machine B to produce a package of bolts. He earns a profit of Rs. 24 per package on nuts and Rs. 18 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 10 hours a day. Make an L.P.P. from above and solve it graphically ?
View SolutionA manufacture makes two types of cups A and B. Three machines are required to manufacture the cups and the time in minutes required by each in as given below:

Each machine is available for a maximum period of 6 hours per day. If the profit on each cup A is 75 paisa and on B is 50 paisa, find how many cups of each type should be manufactures to maximise the profit per day.View Solution

